Underlake Reading Room

这里是图书馆外的阅览室🌟

0%

关于stat的笔记 - estimation

Posted on Edited on In Disqus: 38k 35 mins.

为stat331附录的estimation相关代码.




Simple Linear Regression

yi=β0+β1∗xi+εi,εi∼N(0,σ)y_i =β_0 +β_1*x_i +ε_i, ε_i ∼N(0,σ )

我们通过Least Squares Estimation来estimateβ0β_0和β1β_1.
(省略证明的步骤)

β1LS^=∑(yi−yˉ)(xi−xˉ)∑(xi−xˉ)2\hat{β_1 ^{LS}} = \frac{\sum (y_i - \bar{y})(x_i - \bar{x})}{\sum (x_i - \bar{x})^2} β1LS^=SxySxx\hat{β_1 ^{LS}} = \frac{S_{xy}}{S_{xx}} β0LS^=yˉ−β1LS^\hat{β_0 ^{LS}} = \bar{y} - \hat{β_1 ^{LS}}

Maximum Likelihood Estimation和Least Squares Estimation估算的β0β_0和β1β_1是一样的.

σ^ML2=∑i=1nei2n\hat{σ}_{ML}^2=\frac{\sum_{i=1}^ne_i^2}{n} σ^2=∑i=1nei2n−2\hat{σ}^2=\frac{\sum_{i=1}^ne_i^2}{n-2}

当n大于50时,这两个没什么区别.



注: Sxy=∑(xi−(ˉx))(yi−(ˉy))S_{xy} = \sum (x_i - \bar(x))(y_i - \bar(y))
同理 Sxx=∑(xi−(ˉx))2S_{xx} = \sum (x_i - \bar(x))^2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#--------------------------------------------------------------------------
# lecture 2
#--------------------------------------------------------------------------
## correlation demo:
N <- 2000 ## sample size
b0 <- 0   ## intercept
b1 <- 0.5 ## slope
sig <- 0.2 ## sd of errors (sigma)

## generate data
x <- rnorm(N,0,1) ## covariates
y <- rnorm(N,b0+b1*x,sig) ## outcomes
y2 <- 2*y

par(mfrow=c(1,2))
plot(y~x,xlim=c(-4,4),ylim=c(-3,3)) ## scatterplot
abline(b0,b1,lwd=2,col="blue") ## true line
round(cor(y,x),2) ## correlation

plot(y2~x,xlim=c(-4,4),ylim=c(-3,3)) ## scatterplot
abline(b0,2*b1,lwd=2,col="blue") ## true line
round(cor(y2,x),2) ## correlation



#-------------------------------
### Back to Data
# load Dr. Gladstone's brain data
brain <- read.csv(file = "brainhead.csv")
head(brain) # take a peek at the data
summary(brain) # summarize the data
# create variable names that require less typing
x <- brain$head.size # head size
y <- brain$brain.wgt # brain weight

# histograms
par(mfrow=c(1,2))
hist(x,main="Head Size (cm^3)")
hist(y,main="Brain Weight (grams)")
par(mfrow=c(1,1))

### point estimates for beta0, beta1, and sigma
# prepare some quantities
xbar <- mean(x)
ybar <- mean(y)
Sxy <- sum( (y-ybar) * (x-xbar) )
Sxx <- sum( (x-xbar)^2 )
n <- length(y) # number of observations

# beta1 (MLE)
b1.hat <- cov(y,x)/var(x) # quick way: sample covar. / sample var.
c(b1.hat, Sxy/Sxx) # compare to longer way

# beta0 (MLE)
b0.hat <- ybar - b1.hat * xbar

# sigma2 (Unbiased estimate)
yfit <- b0.hat + b1.hat * x # fitted values
e <- y - yfit # residuals
sig2.hat <- sum(e^2)/(n-2)
sig.hat <- sqrt(sig2.hat)

# display
round(c(b0.hat,b1.hat,sig.hat),3)

# OLS using built-in R functions
# 做model

M <- lm(y ~ x) # fit (l)inear (m)odel
M
# The return object is called a list
typeof(M)
names(M) # see ?lm for meaning of each element

# regression coefficients (betas)
round(M$coefficients,3) # access via list element
round(coef(M),3) # access via accessor function.  see ?lm for others.
round(c(b0.hat, b1.hat),3)




Confidence Intervals

注意confidence intervals分为知道sigma和不知道sigma.
知道sigma用normal distribution,不知道用t distribution.

通过MLE的distribution得知

Z=β1^−β1σ/Sxx∼N(0,1)Z = \frac{\hat{\beta_1} - \beta_1}{\sigma / \sqrt{S_{xx}}} ∼N(0,1) V=1σ2∑i=1nei2∼Xn−22V = \frac{1}{\sigma^2}\sum_{i=1}^n e_i^2 ∼X_{n-2}^2

在知道sigma的情况下,95%的β1=β1^±1.96σSxx\beta_1 = \hat{\beta_1} \pm 1.96\frac{\sigma}{\sqrt{S_{xx}}}
1.96是Z常数.

不知道sigma的情况下,我们使用β1^−β1σ^/Sxx∼tn−22\frac{\hat{\beta_1} - \beta_1}{\hat{\sigma} / \sqrt{S_{xx}}} ∼t_{n-2}^2,95%的β1=β1^±qσ^Sxx\beta_1 = \hat{\beta_1} \pm q\frac{\hat{\sigma}}{\sqrt{S_{xx}}}
q由r计算.写作t1−α/2,n−2t_{1-\alpha/2,n-2}

1
qt(p = 0.05/2, df = n-2, lower.tail = FALSE)

虽然老师讲了很多的代码但不如直接用r自带的confint built-in function好了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

conf <- 0.95 # size of confidence interval (1-alpha)
qval <- -qt(p = (1-conf)/2, df = n-2) # inverse-cdf of a t(n-2)
qval <- qt(p = (1-conf)/2, df = n-2, lower.tail = FALSE)

# CI for beta1
s1 <- sig.hat / sqrt(Sxx) # standard error

b1.CI <- b1.hat + c(-1,1) * qval * s1 # confidence interval
names(b1.CI) <- c("L", "U")
round(b1.CI,digits=3)


# CI for beta0
s0 <- sig.hat * sqrt(1/n + xbar^2/Sxx) # standard error

b0.CI <- b0.hat + c(-1,1) * qval * s0
names(b0.CI) <- c("L", "U")
round(b0.CI,digits=3)

# Compare to built-in functions
confint(M)




Hypothesis Testing

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# H0: beta1 = 0
# test statistic: T = beta1.hat/s1
# T | H0 ~ t_(n-2)
# pval = P( |T| > |Tobs|  |  H0 )

Tobs <- b1.hat/s1 # observed value of test statistic
Tobs

# want P(|T| > |Tobs| | H0)
pval <- pt(q = abs(Tobs),               # |Tobs|
           df = n-2,                    # degrees of freedom
           lower.tail = FALSE)          # return P( T > |Tobs|)
pval <- 2*pval                          # add P( T < |Tobs|)
pval

# compare to built in function
summary(M)



Multiple Linear Regression

也就是多个系数的model.

其中有系数是categorical的,需要特殊处理.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

#--- categorical predictors ------------------------------------------------
# data
mercury <- read.csv("fishermen_mercury.csv")
head(mercury)

# predict MeHg as a function of weight and fishpart
M <- lm(MeHg ~ weight + fishpart, data = mercury)
summary(M)

# since fishpart is coded as:
# None = 0, Muscle = 1, Muscle/Whole = 2, Whole = 3
# model assumes increase in expected MeHg from None to Muscle is
# exactly equal to increase in expected MeHg from Muscle to Muscle/Whole.
# Imagine if we encoded: None = 0, M = 10, MW = 11, W = 20?

# the "design matrix" X for the problem
head(model.matrix(M))

#--- fishpart as categorical predictor -------------------------------------

# convert fishpart to non-numeric categorical variable
fishpart2 <- mercury$fishpart
table(fishpart2)

# "levels" of variable fishpart
fplevels <- c("none", "muscle", "muscle_whole", "whole")
# using for-loop
for(ii in 0:3) {
  fishpart2[fishpart2 == ii] <- fplevels[ii+1]
}
# without for-loop
all(fplevels[mercury$fishpart+1] == fishpart2)


# in R, categorical variables are coded as "factor" variables
tmp <- factor(fishpart2)
head(tmp)
levels(tmp) # alphabetical group ordering

fishpart2 <- factor(fishpart2, levels = fplevels) # custom ordering
levels(fishpart2)

mercury$fishpart <- fishpart2 # replace in dataset

# run regression in R:
Mb <- lm(MeHg ~ weight + fishpart, data = mercury) # intercept model (I)
Mc <- lm(MeHg ~ weight + fishpart - 1,         # no-intercept model (0)
         data = mercury)          # note the "-1" to remove intercept



# compare design matrices at selected values
ind <- c(102, 35, 2, 1, 14, 106)

mercury[ind, c("MeHg", "weight", "fishpart")] # original dataset
model.matrix(Mb)[ind,] # with intercept model
model.matrix(Mc)[ind,] # no intercept model

# interpretation of parameters:
coef(Mb)
# fishpartmuscle: estimate of E[MeHg | ...]

coef(Mc)
# fishpartmuscle: estimate of ...

# note that model predictions are identical:
range(predict(Mb) - predict(Mc))

<figure class="highlight r"><table><tr><td class="gutter"><pre><span class="line">1</span><br><span class="line">2</span><br><span class="line">3</span><br></pre></td><td class="code"><pre><span class="line"></span><br><span class="line">&lt;img src=<span class="string">&quot;/blog/2021/05/12/P194/P194_12.png&quot;</span> <span class="built_in">class</span>=<span class="string">&quot;&quot;</span>&gt;</span><br><span class="line"></span><br></pre></td></tr></table></figure>

<p>#— Hypothesis testing —————————————————-</p>
<h1 id="Question-How-to-test-H0-fishpart-not-associated-with-mercury-in-presence-of-weight"><a href="#Question-How-to-test-H0-fishpart-not-associated-with-mercury-in-presence-of-weight" class="headerlink" title="Question: How to test H0: fishpart not associated with mercury in presence of weight?"></a>Question: How to test H0: fishpart not associated with mercury in presence of weight?</h1><p>Mfull &lt;- lm(MeHg ~ fishpart + weight, data = mercury) # full model<br>coef(Mfull)</p>
<h1 id="degrees-of-freedom"><a href="#degrees-of-freedom" class="headerlink" title="degrees of freedom"></a>degrees of freedom</h1><p>dff &lt;- Mfull$df</p>
<h1 id="F-statistic-using-subset-of-MLE-of-full-model-betastar"><a href="#F-statistic-using-subset-of-MLE-of-full-model-betastar" class="headerlink" title="F-statistic using subset of MLE of full model (betastar)"></a>F-statistic using subset of MLE of full model (betastar)</h1><p>betastar.ind &lt;- 2:4 # indices corresponding to beta’s for fishpart<br>betastar.hat &lt;- coef(Mfull)[betastar.ind] # subset of MLE</p>
<h1 id="vcov-Mfull-sigma-hat-2-X’X-1"><a href="#vcov-Mfull-sigma-hat-2-X’X-1" class="headerlink" title="vcov(Mfull) = sigma.hat^2 * (X’X)^{-1}"></a>vcov(Mfull) = sigma.hat^2 * (X’X)^{-1}</h1><p>betastar.ve &lt;- vcov(Mfull)[betastar.ind,betastar.ind] # betastar.ve = sigma.hat^2 * V</p>
<h1 id="long-hand-calculation"><a href="#long-hand-calculation" class="headerlink" title="long hand calculation"></a>long hand calculation</h1><p>X &lt;- model.matrix(Mfull) # design matrix for full model<br>V &lt;- solve(crossprod(X))[betastar.ind,betastar.ind] # crossprod(X) = t(X) %*% X<br>range(betastar.ve - sigma(Mfull)^2 * V)</p>
<h1 id="Fobs-betastar-hat’-V-1-betastar-hat-q-sigma-hat-2"><a href="#Fobs-betastar-hat’-V-1-betastar-hat-q-sigma-hat-2" class="headerlink" title="Fobs = (betastar.hat’ V^{-1} betastar.hat / q) / sigma.hat^2"></a>Fobs = (betastar.hat’ V^{-1} betastar.hat / q) / sigma.hat^2</h1><h1 id="note-betastar-ve-already-includes-the-denominator"><a href="#note-betastar-ve-already-includes-the-denominator" class="headerlink" title="note: betastar.ve already includes the denominator"></a>note: betastar.ve already includes the denominator</h1><p>Fobs &lt;- t(betastar.hat) %*% solve(betastar.ve, betastar.hat) / length(betastar.hat)</p>
<h1 id="p-value-large-values-of-Fobs-are-more-evidence-against-H0"><a href="#p-value-large-values-of-Fobs-are-more-evidence-against-H0" class="headerlink" title="p-value: large values of Fobs are more evidence against H0"></a>p-value: large values of Fobs are more evidence against H0</h1><p>pf(Fobs, df1 = length(betastar.hat), df2 = dff, lower.tail = FALSE)</p>

其中系数也可能有nolinear的情况.

插播stat444老师的名言:
all models are false but some are useful.

在Assignment1中的例子,按照scatter plot看出跟exponential像,所以plot exponential.

1
2
3
4
5
6
log.sigma2.y = log(sigma2.y)
plot(Week.x, log.sigma2.y , pch=19, cex.axis = 1.5, cex.lab = 1.5, ylim=c(0,12))
var.model = lm(log.sigma2.y ~ Week.x) # exponential
abline(var.model , col="blue" , lwd = 1.5) #从log(y)中求出系数
summary(model)

1
2
3
4
5
6
7
8
9
plot(Week.x, sigma2.y , pch=19, cex.axis = 1.5, cex.lab = 1.5, ylim=c(0,36000))
var.model.exp = function(x,
  a0 = var.model$coeffient[1],
  a1 = var.model$coeffient[2]){
    return(exp(a0+a1*x))
  } # 提取a0和a1
x.plot = seq(1, 17, length = 100)
y.plot = var.model.exp(x.plot)
lines(y.plot~x.plot, col="blue", lwd=1.5) #再plot

从R-squared中看出数据比较大(偏差比较大),model可以再优化.




ANOVA

(这个在stat系列中有记载过,再次备份一下)
ANOVA: How much of the variability in Y is explained by our model?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
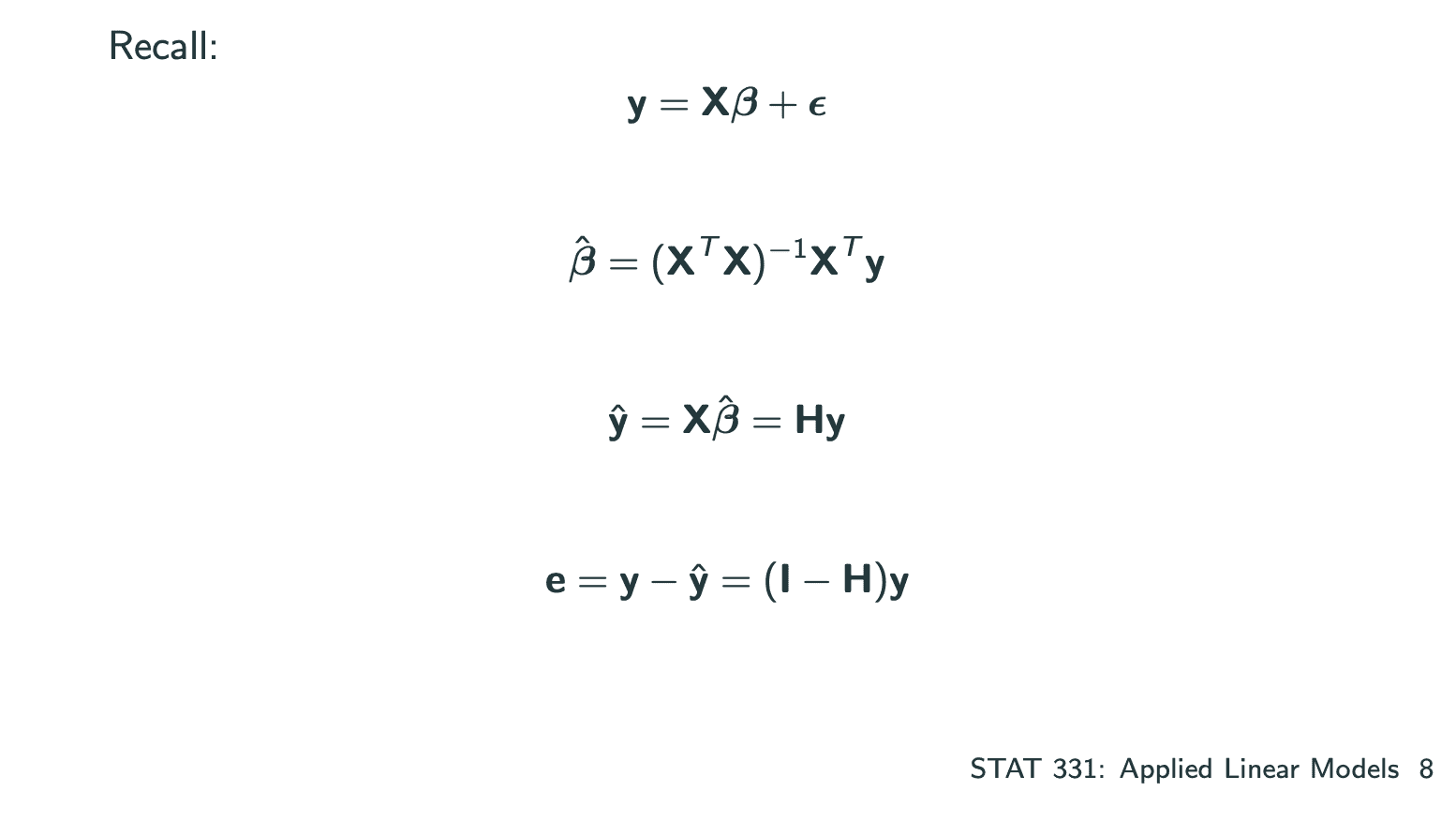
44
### LECTURE 11
#--- first make categorical predictors (from previous lectures) ------------------------------------------------
# data
mercury <- read.csv("fishermen_mercury.csv")
head(mercury)

# predict MeHg as a function of weight and fishpart
M <- lm(MeHg ~ weight + fishpart, data = mercury)
summary(M)

# since fishpart is coded as:
# None = 0, Muscle = 1, Muscle/Whole = 2, Whole = 3
# model assumes increase in expected MeHg from None to Muscle is
# exactly equal to increase in expected MeHg from Muscle to Muscle/Whole.
# Imagine if we encoded: None = 0, M = 10, MW = 11, W = 20?

# the "design matrix" X for the problem
head(model.matrix(M))

#--- fishpart as categorical predictor -------------------------------------

# convert fishpart to non-numeric categorical variable
fishpart2 <- mercury$fishpart
table(fishpart2)

# "levels" of variable fishpart
fplevels <- c("none", "muscle", "muscle_whole", "whole")
# using for-loop
for(ii in 0:3) {
  fishpart2[fishpart2 == ii] <- fplevels[ii+1]
}
# without for-loop
all(fplevels[mercury$fishpart+1] == fishpart2)


# in R, categorical variables are coded as "factor" variables
tmp <- factor(fishpart2)
head(tmp)
levels(tmp) # alphabetical group ordering

fishpart2 <- factor(fishpart2, levels = fplevels) # custom ordering
levels(fishpart2)

mercury$fishpart <- fishpart2 # replace in dataset
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20


#--- ANOVA ----------------------------------------------------

# Fit model
M1 <- lm(MeHg ~ fishpart + weight, data = mercury) #

## ANOVA Decomposition
SSTotal <- sum((mercury$MeHg-mean(mercury$MeHg))^2)
SSReg <- sum((fitted(M1)-mean(mercury$MeHg))^2)
R2 <- SSReg/SSTotal
SSRes <- sum((mercury$MeHg-fitted(M1))^2)
round(SSTotal,10)==round(SSReg+SSRes,10)

# F test for all covariates
# testing \beta_1=\beta_2=\beta_3=\beta_4=0
n <- nrow(mercury)
Fobs <- (SSReg/4)/(SSRes/(n-5)) ## by hand
pf(Fobs,4,n-5,lower.tail=F)
summary(M1) ## R fn
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


#--- F test  ----------------------------------------------------

# Question: How to test H0: fishpart has no effect in presence of weight?

# full model:
Mfull <- lm(MeHg ~ factor(fishpart) + weight, data = mercury)

# reduced model: all levels of fishpart have same intercept
Mred <- lm(MeHg ~ weight, data = mercury)

# degrees of freedom in full and reduced models
dff <- Mfull$df
dfr <- Mred$df

# F-statistic, using LR definition
SSRes_full <- sum(residuals(Mfull)^2) # sum-of-squares for Mfull
SSRes_red <- sum(residuals(Mred)^2) # sum-of-squares for Mred
Fobs <- (SSRes_red-SSRes_full)/(dfr-dff) / (SSRes_full/dff)
c(Fobs, (SSRes_red-SSRes_full)/(dfr-dff) / sigma(Mfull)^2) # equivalent denominator

# F-statistic using subset of MLE of full model
beta.ind <- 2:4 # indices corresponding to beta's for fishpart
beta.hat <- coef(Mfull)[beta.ind] # subset of MLE
beta.ve <- vcov(Mfull)[beta.ind,beta.ind] # beta.ve = sigma.hat^2 * V
Fobs2 <- t(beta.hat) %*% solve(beta.ve, beta.hat) / length(beta.hat)

# check two version are identical
c(Fobs, Fobs2)

# p-value: large values of Fobs are more evidence against H0
pf(Fobs, df1 = (dfr-dff), df2 = dff, lower.tail = FALSE)

# fully R version:
anova(Mred, Mfull)




Goodness of Fit

测试一个model是否合适可以通过测试以下数据:

R2R^2,whereR2=SSRegSSTot=1−SSResSSTotR^2 = \frac{SSR_{eg}}{SST_{ot}} = 1 - \frac{SSR_{es}}{SST_{ot}}.

Interpretation: proportion of variability explained by the model.
Problem: will never decrease when adding more variables.

因此可以测试AdjustedR2R^2.

此外也可以测试AIC.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

library(mvtnorm)
nn <- 200 # n obs
n.cov <- 20 # 20 covs
n.cov.plot <- 20
X <- rmvnorm(nn,rep(0,n.cov),diag(rep(1,n.cov)))
## generate y as function of first 4 covs
y <- X[,1]+X[,2]+X[,3]+X[,4]+rnorm(nn,0,1)
dat <- data.frame(y,X)
# calculate R^2 and R^2_adj upon adding in garbage predictors one at a time
R2 <-  rep(NA,n.cov.plot-1)
R2a <- rep(NA, n.cov.plot-1)
aic <- rep(NA, n.cov.plot-1)
bic <- rep(NA, n.cov.plot-1)
mse <- rep(NA, n.cov.plot-1)
for(ii in 2:n.cov.plot) {
  M <- lm(y ~ ., data = dat[,1:ii])
  R2[ ii-1] <- summary(M)$r.squared
  R2a[ii-1] <- summary(M)$adj.r.squared
  aic[ii-1] <- AIC(M)
  bic[ii-1] <- BIC(M)
  mse[ii-1] <- sigma(M)  
}



plot(2:n.cov.plot, mse, xlab = "# of Predictors", ylab = "",
     main = "MSE",
     pch = 16, type = "b")

plot(2:n.cov.plot, R2, xlab = "# of Predictors", ylab = "",
     main = "Coefficient of Determination",
     pch = 16, type = "b", ylim = range(R2, R2a))
points(2:n.cov.plot, R2a, pch = 16, type = "b", col = "red")
legend(x = "bottomright", legend = expression(R^2, R[adj]^2),
       fill = c("black", "red"))

plot(2:n.cov.plot, aic, xlab = "# of Predictors", ylab = "",
     main = "Criteria",pch = 16, type = "b", ylim = range(aic, bic))
points(2:n.cov.plot, bic, pch = 16, type = "b", col = "blue")
legend(x = "bottomright", legend = expression(AIC, BIC),
       fill = c("black", "blue"))



Automatic Selection

一个model中有多个系数,其中建立model的方式有 将所有的系数一个一个加入 和 一个一个减去 两种,分为Forward Selection和Backward Elimination.

Forward Selection:

Backward Elimination:



还有一种是combine了forward和backward,Stepwise Selection.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# ------ automatic selection ------------------


# forward, backward, and stepwise selection

# high school and beyond dataset
hsb <- read.csv("HSB2.csv")
hsbm <- hsb[,c(13, 1:6, 10, 7:9)] # math response only

summary(hsbm)

# bounds for model selection
M0 <- lm(math ~ 1, data = hsbm) # minimal model

Mfull <- lm(math ~ ., data= hsbm) # full model

# forward
system.time({
Mfwd <- step(object = M0, # base model
             scope = list(lower = M0, upper = Mfull), # smallest and largest model
             trace = 1, # trace prints out information
             direction = "forward" )
})

# backward
system.time({
Mback <- step(object = Mfull, # base model
              scope = list(lower = M0, upper = Mfull),
              direction = "backward", trace = 1)
})

# stepwise (both directions)
system.time({
Mstep <- step(object = M0,
              scope = list(lower = M0, upper = Mfull),
              direction = "both", trace = 1)
})






Cross-validation

cross validation的思想是把数据分组,一部分作为training set,来fit model,一部分作为test set,用来测试fit的model的误差.

k-fold cross validation是其中的一种:将k-1组作为traning set.

leave-one-out cross validation则除了一个数据外将全部数据作为traning set,再计算其中的误差.

load data and fit models from lec 14:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# high school and beyond dataset
hsb <- read.csv("HSB2.csv")
hsbm <- hsb[,c(13, 1:6, 10, 7:9)] # math response only

summary(hsbm)

# bounds for model selection
M0 <- lm(math ~ 1, data = hsbm) # minimal model

# full model:
# 1. remove all interactions with career, but leave as main effect
# 2. remove the interaction between lang and minor
# 3. add nonlinear effects for continuous variables locus, concept, mot
Mfull <- lm(math ~ (.-career)^2 + career - lang:minor +    
            I(locus^2) + I(concept^2) + I(mot^2),
            data= hsbm)
length(coef(Mfull))
anyNA(coef(Mfull))

df.penalty <- 2 # this is the k penalty
## 2 corresponds to AIC
## log(n) corresponds to BIC

# forward
system.time({
  Mfwd <- step(object = M0, # base model
               scope = list(lower = M0, upper = Mfull), # smallest and largest model
               direction = "forward",
               trace = 0, # trace prints out information
               k = df.penalty
  )
})

# backward
system.time({
  Mback <- step(object = Mfull, # base model
                scope = list(lower = M0, upper = Mfull),
                direction = "backward", trace = 0, k = df.penalty)
})

# stepwise (both directions)
Mstart <- lm(math ~ ., data = hsbm) # starting point model: main effects only
system.time({
  Mstep <- step(object = Mstart,
                scope = list(lower = M0, upper = Mfull),
                direction = "both", trace = 1, k = df.penalty)
})

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

# compare Mfull to Mstep
M1 <- Mfull
M2 <- Mstep
Mnames <- expression(M[FULL], M[STEP])

# number of cross-validation replications
nreps <- 1e3

ntot <- nrow(hsbm) # total number of observations
ntrain <- 500 # for fitting MLE's
ntest <- ntot-ntrain # for out-of-sample prediction

# storage space
mspe1 <- rep(NA, nreps) # mspe for M1
mspe2 <- rep(NA, nreps) # mspe for M2

system.time({
  for(ii in 1:nreps) {
    if(ii%%100 == 0) message("ii = ", ii)

    train.ind <- sample(ntot, ntrain) # training observations
    # long-form cross-validation
    ## M1.cv <- lm(math ~ read + prog + race + ses + locus + read:prog + prog:ses,
    ##         data = hsbm, subset = train.ind)
    ## M2.cv <- lm(math ~ race + ses + sch + prog + locus + concept +
    #           mot + read + ses:sch + ses:concept + prog:read,
    #         data = hsbm, subset = train.ind)
    # using R functions
    M1.cv <- update(M1, subset = train.ind)
    M2.cv <- update(M2, subset = train.ind)
    # cross-validation residuals
    M1.res <- hsbm$math[-train.ind] - # test observations
      predict(M1.cv, newdata = hsbm[-train.ind,]) # prediction with training data
    M2.res <- hsbm$math[-train.ind] -predict(M2.cv, newdata = hsbm[-train.ind,])
    # mspe for each model
    mspe1[ii] <- mean(M1.res^2)
    mspe2[ii] <- mean(M2.res^2)

  }
})

# compare
par(mfrow = c(1,2))
cex <- 1
boxplot(x = list(mspe1, mspe2), names = Mnames,
        main = "MSPE",
        #ylab = expression(sqrt(bar(SSE)[CV])),
        ylab = expression(MSPE),
        col = c("yellow", "orange"),
        cex = cex, cex.lab = cex, cex.axis = cex, cex.main = cex)
boxplot(x = list(sqrt(mspe1), sqrt(mspe2)), names = Mnames,
        main = "Root MSPE",
        ylab = expression(sqrt(MSPE)),
        ## ylab = expression(SSE[CV]),
        col = c("yellow", "orange"),
        cex = cex, cex.lab = cex, cex.axis = cex, cex.main = cex)



# compare predictions by training set
par(mfrow=c(1,1))
plot(mspe1, mspe2, pch = 16,
     xlab = Mnames[1], ylab = Mnames[2],
     main = "")
abline(a = 0, b = 1, col= "red", lwd = 2)




1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

#--- K-fold cross-validation -----------------------------------------------------

# compare Mfwd to Mstep
M1 <- Mfwd
M2 <- Mstep
Mnames <- expression(M[FWD], M[STEP])

ntot <- nrow(hsbm) # total number of observations

# number of cross-validation replications
Kfolds <- 10

hsbm <- hsbm[sample(ntot),] # permute rows
hsbm$index <- rep(1:Kfolds,each=ntot/Kfolds)

# storage space
mspe1 <- rep(NA, Kfolds) # mspe for M1
mspe2 <- rep(NA, Kfolds) # mspe for M2

system.time({
  for(ii in 1:Kfolds) {

    train.ind <- which(hsbm$index!=ii) # training observations


    # using R functions
    M1.cv <- update(M1, subset = train.ind)
    M2.cv <- update(M2, subset = train.ind)
    # cross-validation residuals
    M1.res <- hsbm$math[-train.ind] - # test observations
      predict(M1.cv, newdata = hsbm[-train.ind,]) # prediction with training data
    M2.res <- hsbm$math[-train.ind] -predict(M2.cv, newdata = hsbm[-train.ind,])
    # mspe for each model
    mspe1[ii] <- mean(M1.res^2)
    mspe2[ii] <- mean(M2.res^2)

  }
})


# compare
par(mfrow = c(1,2))
cex <- 1
boxplot(x = list(mspe1, mspe2), names = Mnames,
        main = "MSPE",
        #ylab = expression(sqrt(bar(SSE)[CV])),
        ylab = expression(MSPE),
        col = c("yellow", "orange"),
        cex = cex, cex.lab = cex, cex.axis = cex, cex.main = cex)
boxplot(x = list(sqrt(mspe1), sqrt(mspe2)), names = Mnames,
        main = "Root MSPE",
        ylab = expression(sqrt(MSPE)),
        ## ylab = expression(SSE[CV]),
        col = c("yellow", "orange"),
        cex = cex, cex.lab = cex, cex.axis = cex, cex.main = cex)


mean(mspe1)
mean(mspe2)



PRESS1 <- resid(M1)/(1-hatvalues(M1))
PRESS2 <- resid(M2)/(1-hatvalues(M2))

# should match if doing LOO-CV
mean(PRESS1^2)
mean(PRESS2^2)



k-fold cross validation stat444加强版:

这里也包括了LOOCV.
一般k-fold有更好的bais和variance trace off,但LOOCV会更快.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
# A function to generate the indices of the k-fold sets
kfold <- function(N, k=N, indices=NULL){
  # get the parameters right:
  if (is.null(indices)) {
    # Randomize if the index order is not supplied
    indices <- sample(1:N, N, replace=FALSE)
  } else {
    # else if supplied, force N to match its length
    N <- length(indices)
  }
  # Check that the k value makes sense.
  if (k > N) stop("k must not exceed N")
  #

  # How big is each group?
  gsize <- rep(round(N/k), k)

  # For how many groups do we need odjust the size?
  extra <- N - sum(gsize)

  # Do we have too few in some groups?
  if (extra > 0) {
    for (i in 1:extra) {
      gsize[i] <- gsize[i] +1
    }
  }
  # Or do we have too many in some groups?
  if (extra < 0) {
    for (i in 1:abs(extra)) {
      gsize[i] <- gsize[i] - 1
    }
  }

  running_total <- c(0,cumsum(gsize))

  # Return the list of k groups of indices
  lapply(1:k,
         FUN=function(i) {
           indices[seq(from = 1 + running_total[i],
                       to = running_total[i+1],
                       by = 1)
                   ]
         }
  )
}


# A function to form the k samples
getKfoldSamples <- function (x, y, k, indices=NULL){
  groups <- kfold(length(x), k, indices)
  Ssamples <- lapply(groups,
                     FUN=function(group) {
                       list(x=x[-group], y=y[-group])
                     })
  Tsamples <- lapply(groups,
                     FUN=function(group) {
                       list(x=x[group], y=y[group])
                     })
  list(Ssamples = Ssamples, Tsamples = Tsamples)
}


set.seed(1234)

# Simulating the data
x = seq(1,10,length=50)
y = 5+log(x)*sin(.65*x)-2*cos(x-5)/(sqrt(x)) + rnorm(50,mean=0,sd=1) #+ c(rnorm(22,mean=0,sd=1) , rnorm(28,mean=0,sd=.4))
SimulatedData = data.frame(x,y)
plot(y~x,pch=19 , col=adjustcolor("brown",0.7) , cex.axis=1.5 , cex.lab=1.5)

# For leave one out cross-validation
samples_loocv <-  getKfoldSamples(SimulatedData$x, SimulatedData$y, k=length(SimulatedData$y))
# 10 fold cross-validation
samples_10fold <-  getKfoldSamples(SimulatedData$x, SimulatedData$y, k=10)
# 5 fold cross-validation
samples_5fold <-  getKfoldSamples(SimulatedData$x, SimulatedData$y, k=5)


# the degrees of freedom associated with each
complexity <- c(1:10) # Thiese are the degrees of polynomials to be fitted

# Performing the Cross-Validation
Ssamples <- samples_5fold$Ssamples # change this accorcing to the number of folds
Tsamples <- samples_5fold$Tsamples # change this accorcing to the number of folds
CV.To.Plot = data.frame(Complexity=NA , MSE=NA)
for(i in 1:length(complexity)){
  MSE = c()
  for(j in 1:length(Ssamples)){
    x.temp = Ssamples[[j]]$x
    y.temp = Ssamples[[j]]$y
    model = lm(y.temp~poly(x.temp , complexity[i]))
    pred = predict(model , newdata=data.frame(x.temp=Tsamples[[j]]$x))
    MSE[j] = mean((Tsamples[[j]]$y-pred)^2)
  }
  CV.To.Plot[i,] = c(complexity[i] , mean(MSE))
}

Title.Graph = "5-fold CV" # change this accorcing to the number of folds
plot(CV.To.Plot , pch=19 , col="darkblue" , type="b",
     cex.axis = 1.5 , cex.lab=1.5 , ylab="Overall CV Error")
indx = which.min(CV.To.Plot$MSE)
abline(v=indx ,lty=2 , lwd=2 , col='red')
title(main=Title.Graph)

plot(y~x,pch=19 , col=adjustcolor("brown",0.7) , cex.axis=1.5 , cex.lab=1.5)
curve(5+log(x)*sin(.65*x)-2*cos(x-5)/(sqrt(x)),
      xlim = c(1, 10), col = "black", add = TRUE)
lines(x, predict(lm(y~poly(x,4))), type="l", col="blue", lwd=2)
text(8,7,"Black: True")
text(8,6.5,"Blue: Fitted" , col="blue")
title(main="")




Linear Regression Assumptions:

  1. Linearity
  2. Independence
  3. Normality
  4. Equal variance (homoskedasticity)

code for checking them:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

### --------Diagnostics in Practice-----------------
library(car)


# high school and beyond dataset
hsb <- read.csv("HSB2.csv")
hsbm <- hsb[1:150,c(13, 1:6, 10, 7:9)] # math response only

## look at data
summary(hsbm)


## fit model
M1 <- lm(math ~ locus + concept + mot , data = hsbm)

## residuals
res1 <- resid(M1) # raw residuals
stud1 <- res1/(sigma(M1)*sqrt(1-hatvalues(M1))) # studentized residuals

## plot distribution of studentized residuals
hist(stud1,breaks=12,
     probability=TRUE,xlim=c(-4,4),
     xlab="Studentized Residuals",
     main="Distribution of Residuals")
grid <- seq(-3.5,3.5,by=0.05)
lines(x=grid,y=dnorm(grid),col="blue") # add N(0,1) pdf

## qqplot of studentized residuals
qqnorm(stud1)
abline(0,1) # add 45 degree line
# 如果qqplot完全normal就会跟45度线重合.

## plot of residuals vs X
plot(res1~hsbm$locus,
     xlab="Locus.",
     ylab="Residuals",
     main="Residuals vs X")
abline(0,0) ## add horizontal line
plot(res1~hsbm$concept,
     xlab="Concept.",
     ylab="Residuals",
     main="Residuals vs X")
abline(0,0) ## add horizontal line
plot(res1~hsbm$mot,
     xlab="Motiv.",
     ylab="Residuals",
     main="Residuals vs X")
abline(0,0) ## add horizontal line

## partial regression (aka added variable plots)
avPlots(M1)

## plot of studentized residuals vs fitted values
plot(stud1~fitted(M1),
     xlab="Fitted Vals",
     ylab="Studentized Residuals",
     main="Residuals vs Fitted")


## standard residual plots
plot(M1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220

##--------Practice Q2 :Simulations------------

## load packages
library(mvtnorm)

## set seed for reproducibility
set.seed(1000)

## set parameters
n <- 300
sig <- 1.5

## generate 4 covariates
X <- data.frame(rmvnorm(n,sigma=matrix(0.5,4,4)+diag(rep(1,4),4,4)))

## generate outcome under different models
y <- rnorm(n,-2+0.8*X$X1,sig) ## linear assoc.
y2 <- rnorm(n,-2+0.8*X$X1^2,sig) ## non-linear assoc.
y3 <- -2+0.8*X$X1+runif(n,-2,2) ## non-gaussian errors
y4 <- rnorm(n,-2+0.8*X$X1,abs((4+X$X1))) ## mean-variance relationship
y5 <- rnorm(n,-2+0.8*X$X1+0.8*X$X1^2+0.4*X$X2+1.2*X$X3,sig) ## MLR

## combine data into data.frame
dat <- data.frame(X,y,y2,y3,y4,y5)


#------Linear Assoc. with Gaussian Errors -------------
## SLR
M1 <- lm(y~X1,data=dat)

## compute  residuals
res1 <- resid(M1) # raw residuals
stud1 <- res1/(sigma(M1)*sqrt(1-hatvalues(M1))) # studentized residuals

## plot distribution of studentized residuals
hist(stud1,breaks=12,
     probability=TRUE,xlim=c(-4,4),
     xlab="Studentized Residuals",
     main="Distribution of Residuals")
grid <- seq(-3.5,3.5,by=0.05)
lines(x=grid,y=dnorm(grid),col="blue") # add N(0,1) pdf

## qqplot of studentized residuals
qqnorm(stud1)
abline(0,1) # add 45 degree line

## plot of residuals vs X
plot(res1~X$X1,
     xlab=expression(X[1]),
     ylab="Residuals",
     main="Residuals vs X")

## plot of studentized residuals vs fitted values
plot(stud1~fitted(M1),
     xlab="Fitted Vals",
     ylab="Studentized Residuals",
     main="Residuals vs Fitted")


#--------Quad. Assoc. and Gaussian Errors-----------------

## SLR (assuming linear assoc.)
M2 <- lm(y2~X1,data=dat)

## compute  residuals
res2 <- resid(M2) # raw residuals
stud2 <- res2/(sigma(M2)*sqrt(1-hatvalues(M2))) # studentized residuals

## plot studentized residuals
hist(stud2,breaks=20,
     probability=TRUE,xlim=c(-4,4),
     xlab="Studentized Residuals",
     main="Distribution of Residuals")
grid <- seq(-3.5,3.5,by=0.05)
lines(x=grid,y=dnorm(grid),col="blue") # add N(0,1) pdf

## qqplot
qqnorm(stud2)
abline(0,1) # add 45 degree line

## plot of residuals vs X
plot(res2~X$X1,
     xlab=expression(X[1]),
     ylab="Residuals",
     main="Residuals vs X")

## plot of studentized residuals vs fitted values
plot(stud2~fitted(M2),
     xlab="Fitted Vals",
     ylab="Studentized Residuals",
     main="Residuals vs Fitted")



#------Non-Gaussian Residuals -------------
## SLR, assuming gaussian errors
M3 <- lm(y3~X1,data=dat)

## compute  residuals
res3 <- resid(M3) # raw residuals
stud3 <- res3/(sigma(M3)*sqrt(1-hatvalues(M3))) # studentized residuals

## plot distribution of studentized residuals
hist(stud3,breaks=12,
     probability=TRUE,xlim=c(-4,4),
     xlab="Studentized Residuals",
     main="Distribution of Residuals")
grid <- seq(-3.5,3.5,by=0.05)
lines(x=grid,y=dnorm(grid),col="blue") # add N(0,1) pdf

## qqplot of studentized residuals
qqnorm(stud3)
abline(0,1) # add 45 degree line

## plot of residuals vs X
plot(res3~X$X1,
     xlab=expression(X[1]),
     ylab="Residuals",
     main="Residuals vs X")

## plot of studentized residuals vs fitted values
plot(stud3~fitted(M3),
     xlab="Fitted Vals",
     ylab="Studentized Residuals",
     main="Residuals vs Fitted")



#------Heteroskedasticity-------------
## SLR
M4 <- lm(y4~X1,data=dat)

## compute  residuals
res4 <- resid(M4) # raw residuals
stud4 <- res4/(sigma(M4)*sqrt(1-hatvalues(M4))) # studentized residuals

## plot distribution of studentized residuals
hist(stud4,breaks=12,
     probability=TRUE,xlim=c(-4,4),
     xlab="Studentized Residuals",
     main="Distribution of Residuals")
grid <- seq(-3.5,3.5,by=0.05)
lines(x=grid,y=dnorm(grid),col="blue") # add N(0,1) pdf

## qqplot of studentized residuals
qqnorm(stud4)
abline(0,1) # add 45 degree line

## plot of residuals vs X
plot(res4~X$X1,
     xlab=expression(X[1]),
     ylab="Residuals",
     main="Residuals vs X")

## plot of studentized residuals vs fitted values
plot(stud4~fitted(M4),
     xlab="Fitted Vals",
     ylab="Studentized Residuals",
     main="Residuals vs Fitted")




#------Linear Assoc. with Gaussian Errors -------------
## SLR
M5 <- lm(y5~X1+X2+X3+X4,data=dat)

## compute  residuals
res5 <- resid(M5) # raw residuals
stud5 <- res5/(sigma(M5)*sqrt(1-hatvalues(M5))) # studentized residuals

## plot distribution of studentized residuals
hist(stud5,breaks=12,
     probability=TRUE,xlim=c(-4,4),
     xlab="Studentized Residuals",
     main="Distribution of Residuals")
grid <- seq(-3.5,3.5,by=0.05)
lines(x=grid,y=dnorm(grid),col="blue") # add N(0,1) pdf

## qqplot of studentized residuals
qqnorm(stud5)
abline(0,1) # add 45 degree line


## plot of studentized residuals vs fitted values
plot(stud5~fitted(M5),
     xlab="Fitted Vals",
     ylab="Studentized Residuals",
     main="Residuals vs Fitted")

## plot of residuals vs X1,X2,X3,X4
plot(res5~X$X1,
     xlab=expression(X[1]),
     ylab="Residuals",
     main="Residuals vs X")
plot(res5~X$X2,
     xlab=expression(X[2]),
     ylab="Residuals",
     main="Residuals vs X")
plot(res5~X$X3,
     xlab=expression(X[3]),
     ylab="Residuals",
     main="Residuals vs X")
plot(res5~X$X4,
     xlab=expression(X[4]),
     ylab="Residuals",
     main="Residuals vs X")


## plot of residuals vs X1,X2,X3,X4
My <- lm(y5~X2+X3+X4,data=dat)
Mx <- lm(X1~X2+X3+X4,data=dat)
plot(My$residuals~Mx$residuals,
     xlab=expression(e[x[1]]),
     ylab=expression(e[y]),
     main="Partial Regression Plot")

avPlots(M5)

在不满足的情况下修改model:

  1. Linearity
  • Instead include log(xj)
  • Instead use a quadratic model (xj and xj2)
  1. Independence
  • Estimates are still unbiased but standard errors are broken
    =⇒ replace SEs with robust alternatives (sandwich form, GEE)
  • Explicitly model the dependence structure • Mixed effects models
  1. Normality

Violations of normality might not be a big deal

  • E.g. if we have a large sample size
    However, Normality is required for valid prediction intervals
  • Could consider transforming Y
    E.g. model log(Y)
    This again changes interpretations!
    Might not be a problem if we’re interested in prediction
  • Could consider other regression approaches: GLMs, etc. (not covered in this course)
  1. Equal variance (homoskedasticity)

If our errors are heteroskedastic, we have a few options:

  • Transform outcome (see above)
    Variance stabilizing transform
  • Weighted Least Squares
  • Bootstrap (time permitting…)

Weighted Least Squares:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
## load packages
library(mvtnorm)

## set seed for reproducibility
set.seed(1000)

## set parameters
n <- 300
sig <- 1.5

## generate 4 covariates
X <- data.frame(rmvnorm(n,sigma=matrix(0.5,4,4)+diag(rep(1,4),4,4)))

## generate outcome under different models
# y <- rnorm(n,-2+0.8*X$X1,sig) ## linear assoc.
y2 <- rnorm(n,-2+0.8*X$X1^2,sig) ## non-linear assoc.
y4 <- rnorm(n,-2+0.8*X$X1,abs((4+X$X1))) ## mean-variance relationship

## combine data into data.frame
dat <- data.frame(X,y,y2,y4)

#--------------------------------
## Linear
Mlin <- lm(y2~X1,data=dat)

## compute  residuals
reslin <- resid(Mlin) # raw residuals
studlin <- reslin/(sigma(Mlin)*sqrt(1-hatvalues(Mlin))) # studentized residuals


## plot of residuals vs X
plot(reslin~X$X1,
     xlab=expression(X[1]),
     ylab="Residuals",
     main="Residuals vs X")

## plot of residuals vs X^2
plot(reslin~I(X$X1^2),
     xlab=expression(X[1]^2),
     ylab="Residuals",
     main="Residuals vs X^2")


#--------------------------------
## Quadratic
Mquad <- lm(y2~X1+I(X1^2),data=dat)

## compute  residuals
resquad <- resid(Mquad) # raw residuals
studquad <- resquad/(sigma(Mquad)*sqrt(1-hatvalues(Mquad))) # studentized residuals

## plot of residuals vs X
plot(resquad~X$X1,
     xlab=expression(X[1]),
     ylab="Residuals",
     main="Residuals vs X")

## plot of residuals vs X^2
plot(resquad~I(X$X1^2),
     xlab=expression(X[1]^2),
     ylab="Residuals",
     main="Residuals vs X^2")



### --------Iteratively Re-Weighted Least Squares--------

#--------------------------------
## OLS
Mols <- lm(y4~X1,data=dat)

## compute  residuals
resols <- resid(Mols) # raw residuals
studols <- resols/(sigma(Mols)*sqrt(1-hatvalues(Mols))) # studentized residuals


## plot of studentized residuals vs fitted values
plot(studols~fitted(Mols),
     xlab="Fitted Vals",
     ylab="Studentized Residuals",
     main="Residuals vs Fitted")

#--------------------------------
## WLS
# step 1
# initial estimates (OLS)
Mcurrent <- lm(y4~X1,data=dat)
Mcurrent$coef

# step 2
# model |e|
abs_resid <- abs(Mcurrent$residuals)
Mresid <- lm(abs_resid~ fitted(Mcurrent))
w <- 1/fitted(Mresid)^2
# fit WLS
Mwls <- lm(y4~X1,weights=w,data=dat)
Mwls$coef

# step 3
Mcurrent <- Mwls
# model |e|
abs_resid <- abs(Mcurrent$residuals)
Mresid <- lm(abs_resid~ fitted(Mcurrent))
w <- 1/fitted(Mresid)^2
# fit WLS
Mwls <- lm(y4~X1,weights=w,data=dat)
Mwls$coef

# step 4
Mcurrent <- Mwls
# model |e|
abs_resid <- abs(Mcurrent$residuals)
Mresid <- lm(abs_resid~ fitted(Mcurrent))
w <- 1/fitted(Mresid)^2
# fit WLS
Mwls <- lm(y4~X1,weights=w,data=dat)
Mwls$coef


### automatically:
sumdiff <- 100 ## initial val
threshold <- 10e-12 ## stopping condition
iter <- 1 ## count iterations
Mcurrent <- lm(y4~X1,data=dat) ## initial OLS fit
while(sumdiff>=threshold){

  # model |e|
  abs_resid <- abs(Mcurrent$residuals)
  Mresid <- lm(abs_resid~ fitted(Mcurrent))
  w <- 1/fitted(Mresid)^2
  # fit WLS
  Mwls <- lm(y4~X1,weights=w,data=dat)

  ## compute differences
  sumdiff <- sum(abs(Mwls$coef-Mcurrent$coef))
  Mcurrent <- Mwls

  ## count iterations
  print(iter)
  iter <- iter+1

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

### --------PQ1: Weighted Least Squares-----------------
library(readr)
hosp <- read_csv("hospitals.csv")

# calculate the weighted regression using matrices
y <- hosp$SurgQual # response
X <- cbind(1, hosp$Difficulty) # covariate matrix
N <- hosp$N # sample sizes

y_W <- y*sqrt(N) # multiply by W^{1/2}
X_W <- X*sqrt(N)# multiply by W^{1/2}
beta.hat.WLS <- c(solve(t(X_W)%*%X_W)%*%t(X_W)%*%y_W) # WLS estimator
beta.hat.WLS

# OLS on pre multiplied data
g_WLS2 <- lm(y_W ~ X_W-1, data = hosp)
g_WLS2$coef

# using the built-in R function
# R expects weights = N, not weights = sqrt(N)
g_WLS <- lm(SurgQual ~ Difficulty, weights = N, data = hosp)
g_WLS$coef

## OLS
g_OLS <- lm(SurgQual ~ Difficulty,  data = hosp)
g_OLS$coef


# plot the data with circle proportional to sample sizes
plot(hosp$Difficulty, hosp$SurgQual,
     xlab = "Case Load Difficulty Index",
     ylab = "Post-Surgery Quality Index",
     cex = sqrt(hosp$N/max(hosp$N))^2*4,
     pch = 16,
     col = "lightgrey")
points(hosp$Difficulty, hosp$SurgQual, pch = 3, col = "black")
abline(g_OLS, col = "blue") # add simple regression line
abline(g_WLS, col = "blue", lty = 2) # add weighted regression line
# add legend to plot
legend(x = "topright",
       legend = c("OLS", "WLS"),
       col = "blue", cex = .8,
       lty = c(1, 2), seg.len = 1)


stat444加强版选择weight: