因为上一篇太乱了没看懂于是新开一篇(靠).
Code
Get Instance.
Action
1 | using UnityEngine.Events; |
RequireComponent
这么写会帮助gameObject绑定寻找需要的component.
1 | [RequireComponent(typeof(CharacterController))] |
GroundCheck
1 | void GroundCheck() |
Unity Events
PlayerInput
1 | private PlayerInput _input; |
Generics
可以用
1 | using UnityEngine; |
1 | using UnityEngine; |
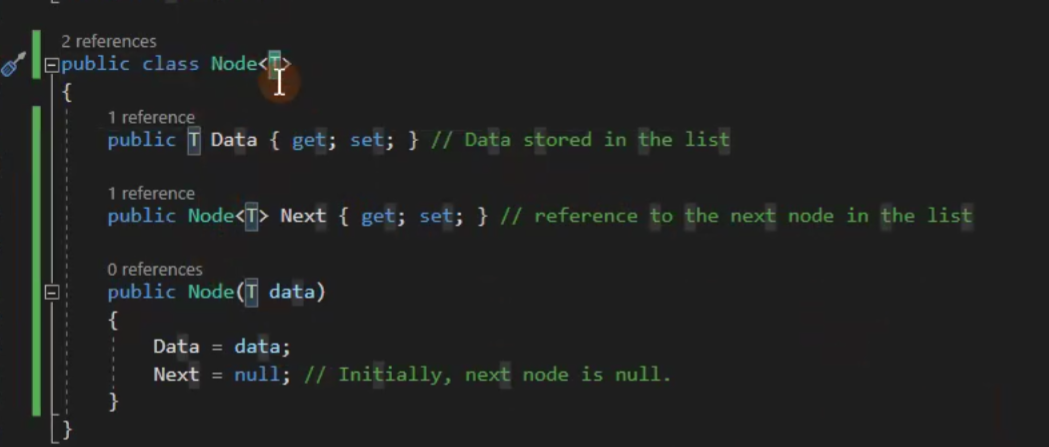
Collision / Trigger
| OnCollisionEnter | OnCollisionEnter is called when this collider/rigidbody has begun touching another rigidbody/collider. |
|---|---|
| OnCollisionExit | OnCollisionExit is called when this collider/rigidbody has stopped touching another rigidbody/collider. |
| OnCollisionStay | OnCollisionStay is called once per frame for every Collider or Rigidbody that touches another Collider or Rigidbody. |
| OnTriggerEnter | When a GameObject collides with another GameObject, Unity calls OnTriggerEnter. |
| OnTriggerExit | OnTriggerExit is called when the Collider other has stopped touching the trigger. |
| OnTriggerStay | OnTriggerStay is called almost all the frames for every Collider other that is touching the trigger. The function is on the physics timer so it won’t necessarily run every frame. |
Joints
也有2Djoints.
Design Pattern
Observer Design Pattern
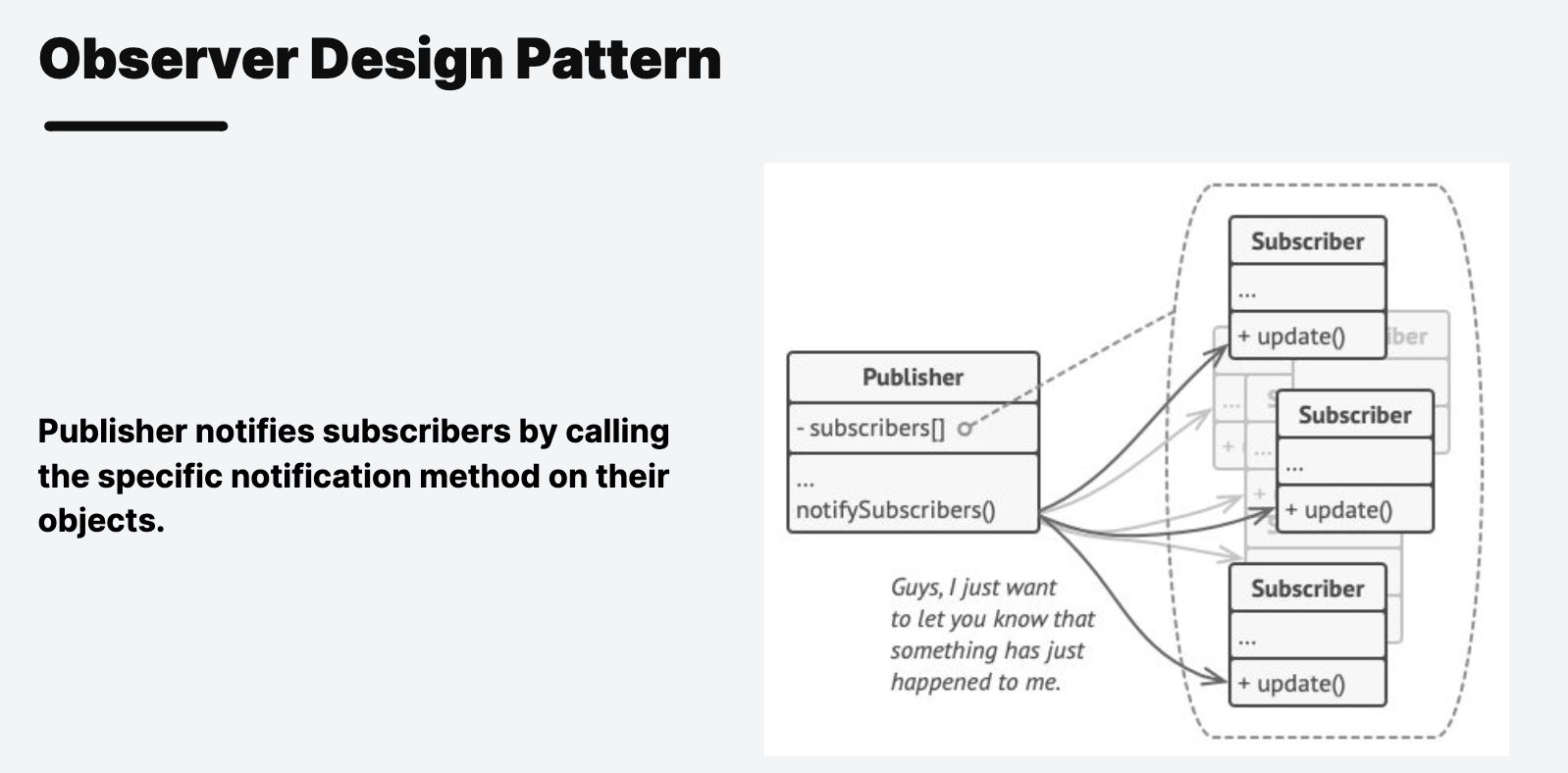
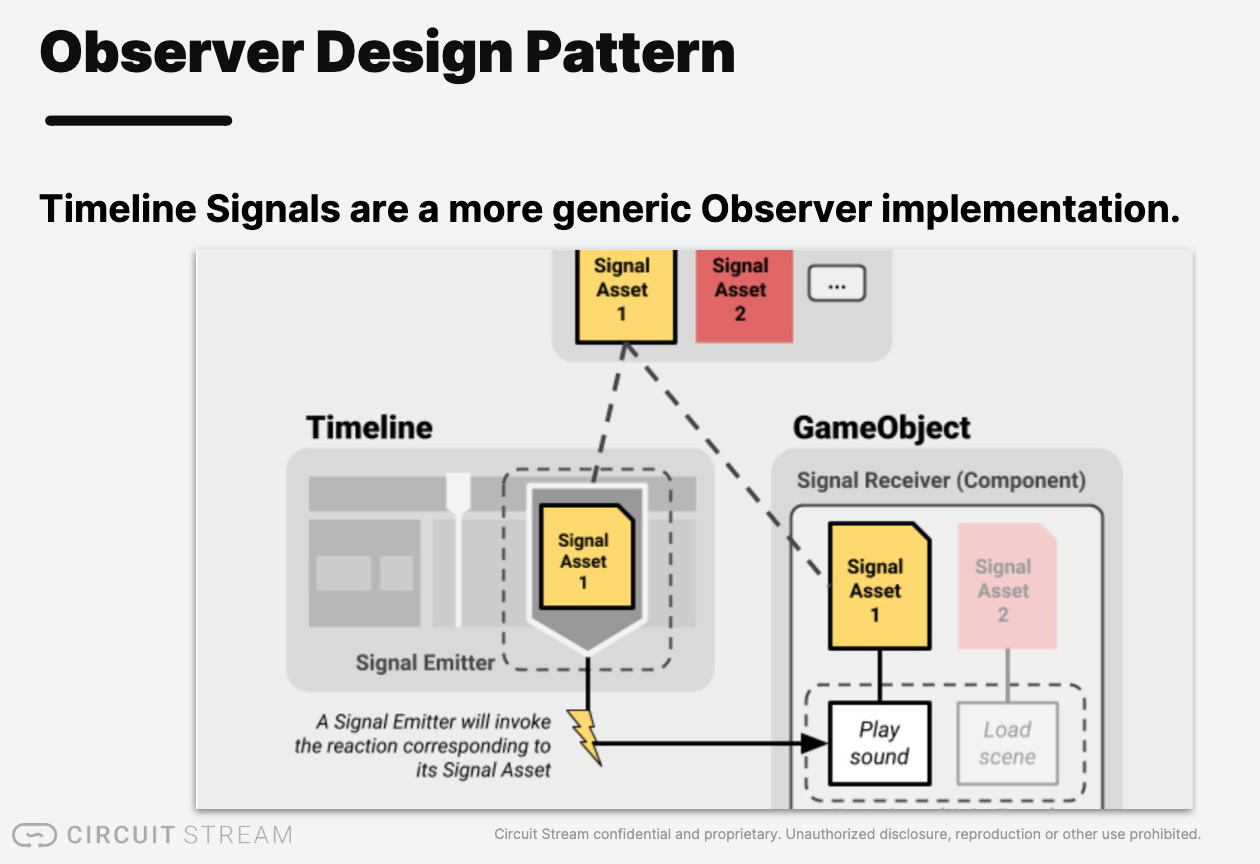
UnityEvents and Actions are Unity-specific implementations of the Observer pattern.
- AddListener and RemoveListener are the subscription functions.
- Invoking the Action/UnityEvent is the notify behavior.
1 | using System; |
The Command Design Pattern
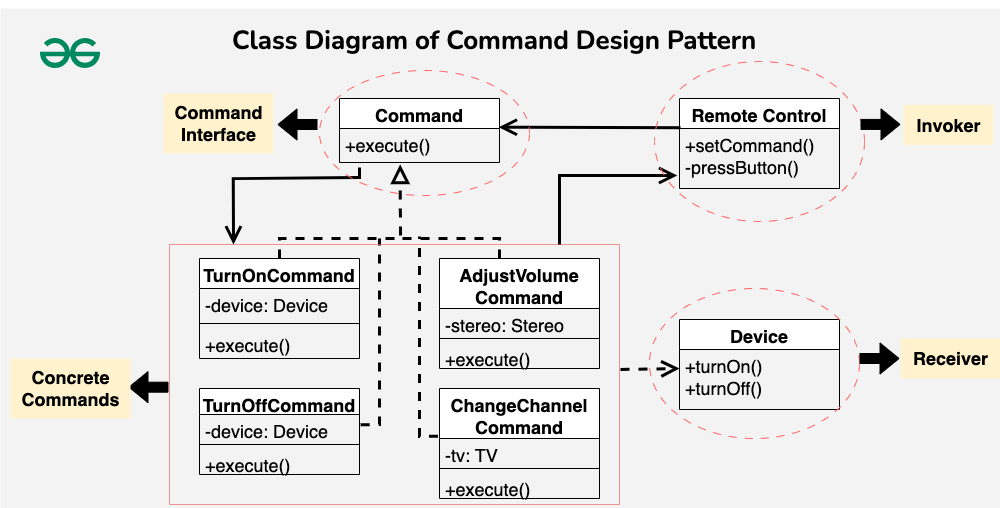
1 | using System; |
Object Pool Design Pattern
Create a pool of instantiated objects, and use them as needed without destroying them, just return them to the pool.
State Design Pattern
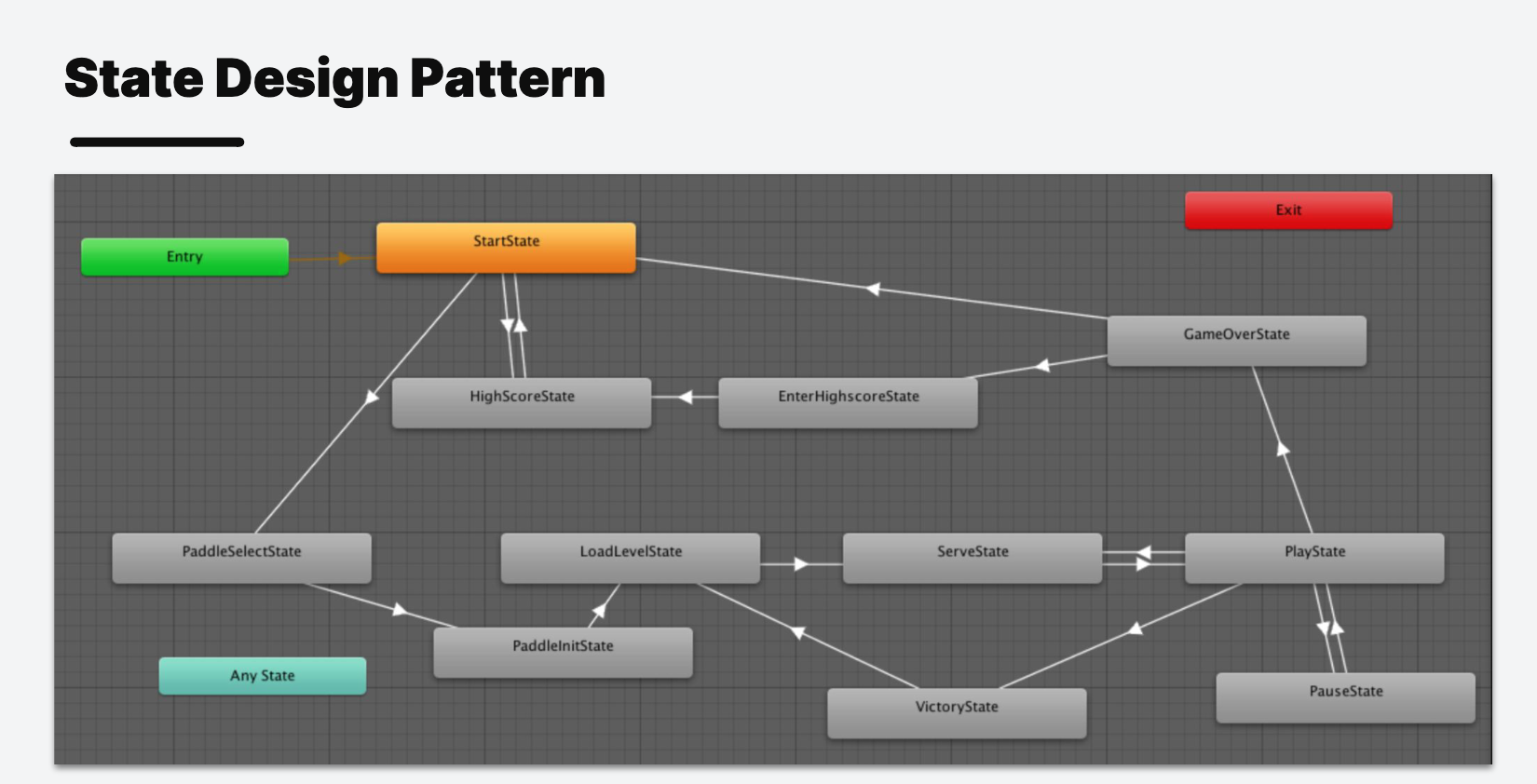
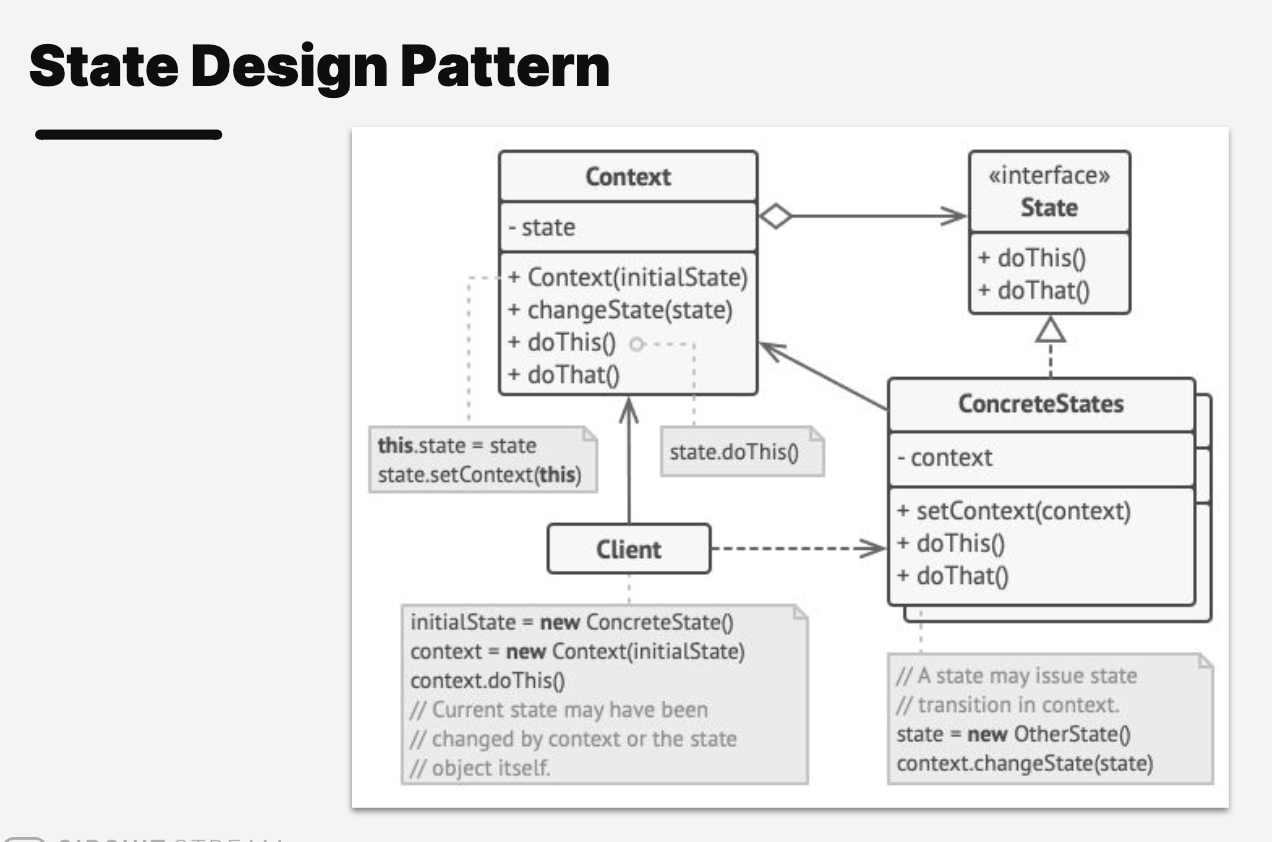
1 | // State interface |
The Strategy Design Pattern
1 | // Strategy interface |
Interactor
这是design pattern吗(何.
1 | public abstract class Interactor : MonoBehaviour |
1 | public class SimpleInteractor : Interactor |
Notes
来看一下Render.
Universal RP
这个在unity 3D universal中自带,但3D core中没有.
导致部分material会出现显示错误(pink).
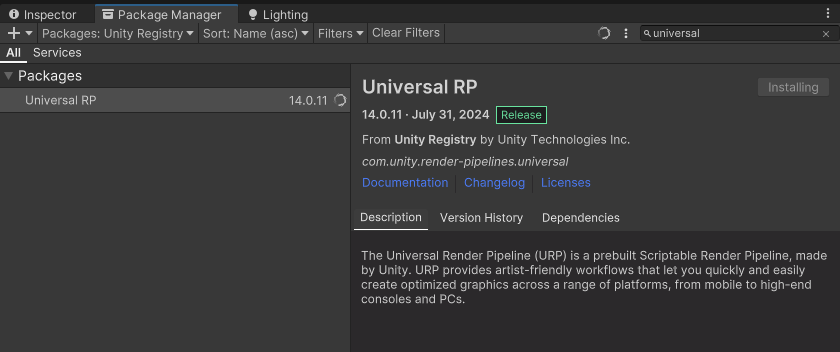
可以把material给成standard或者增添这个package.
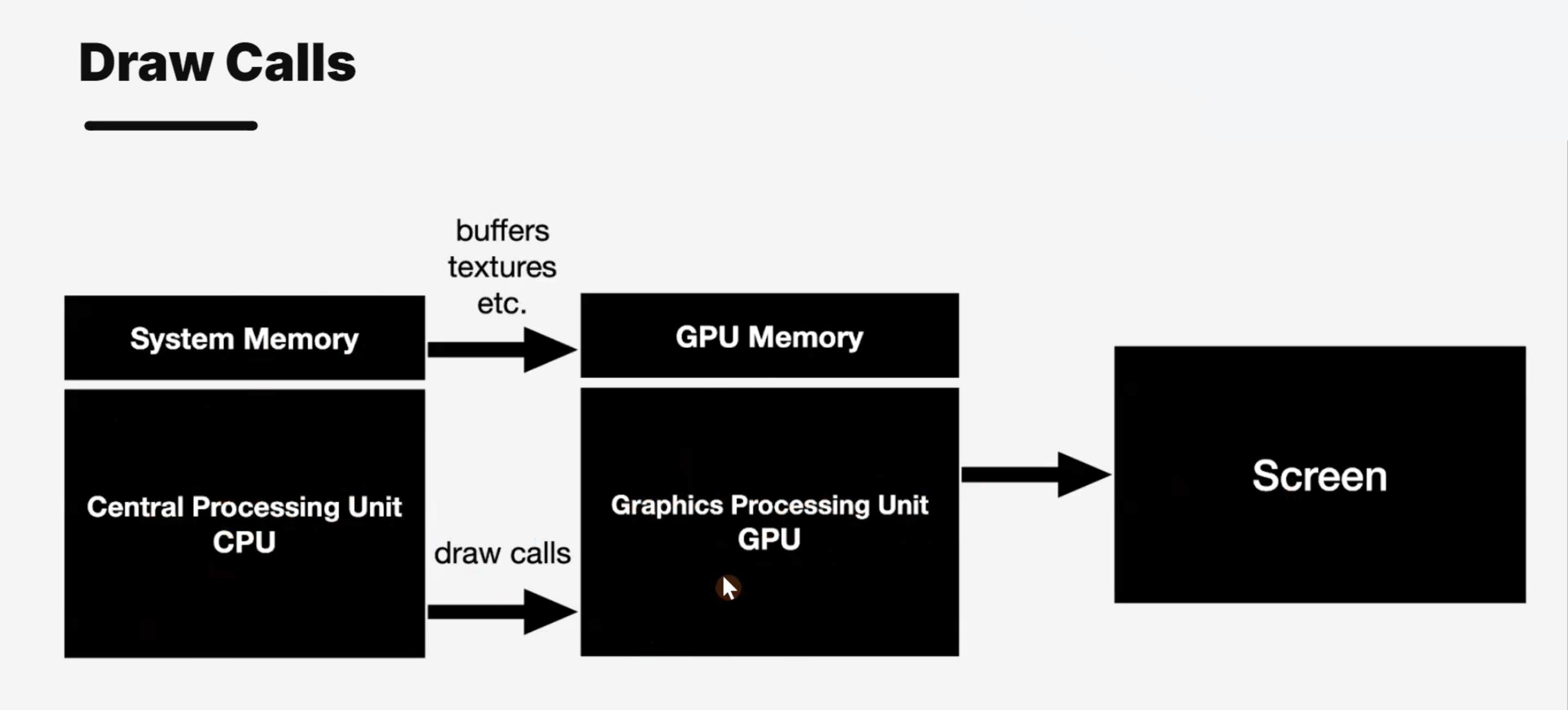
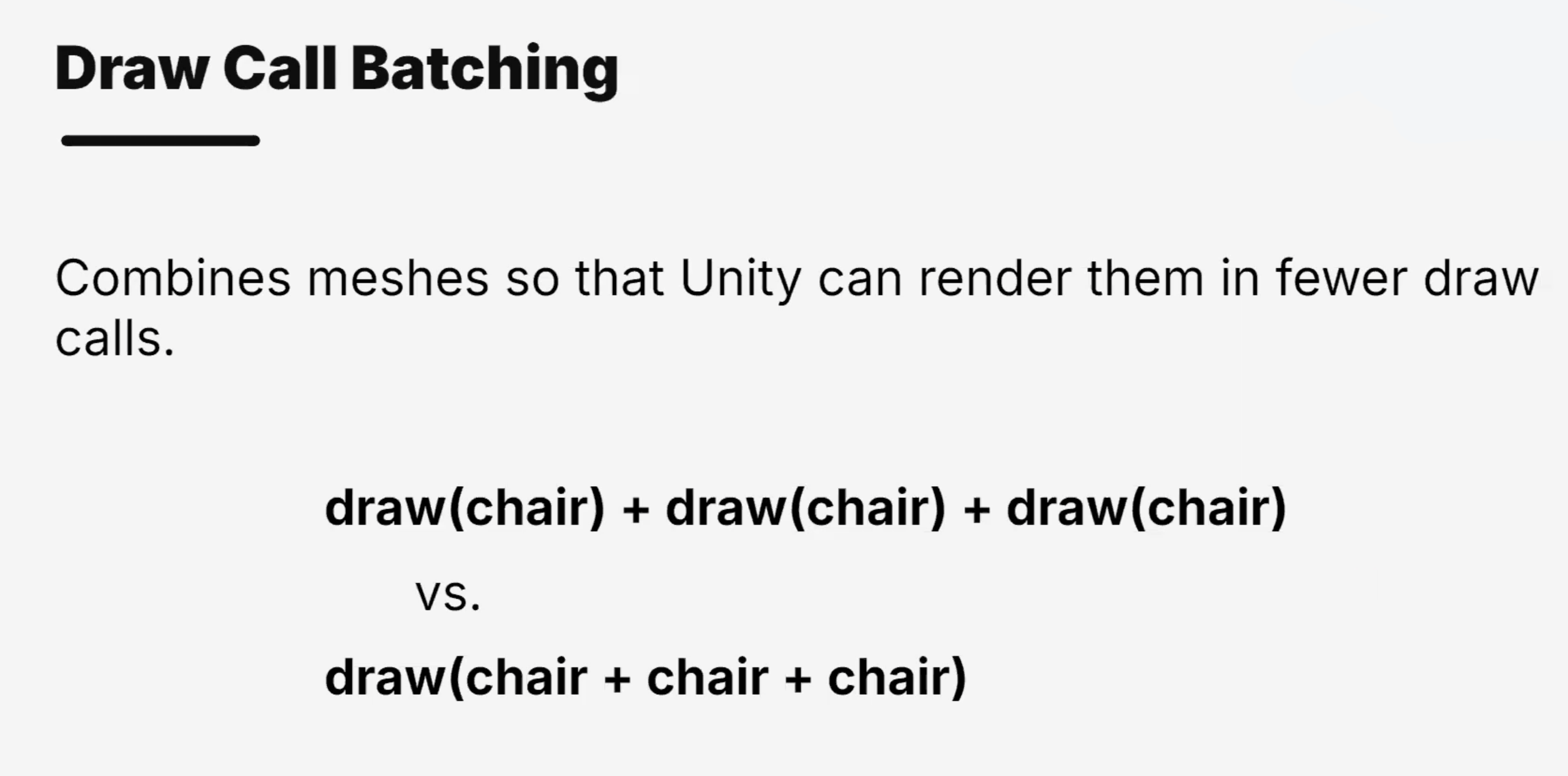
Draw Calls


UV Editing/Mode
what is uv editing??

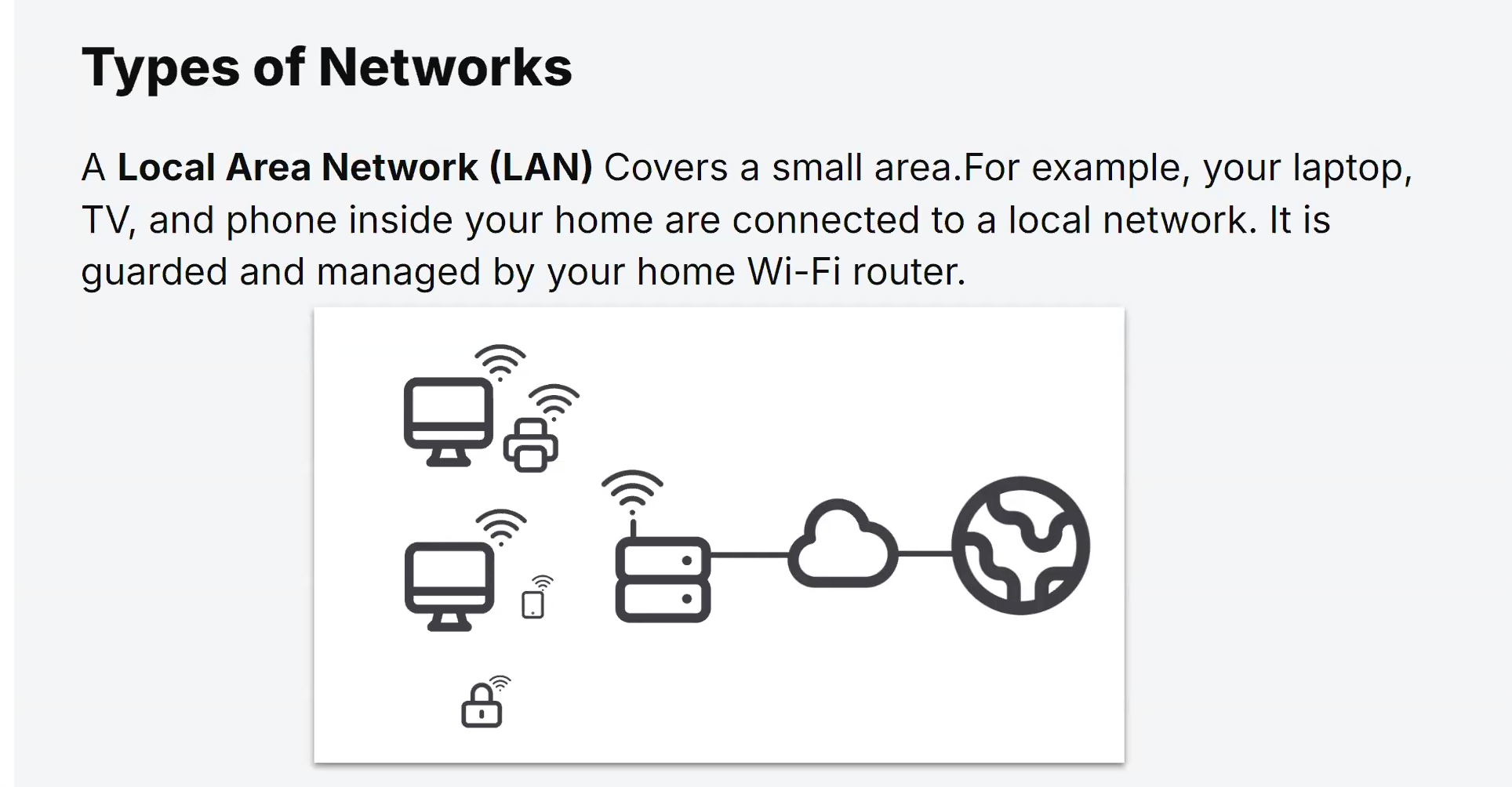
Computer Networks
Latency and Lag
Reducing the delay between a player’s action and the game’s response is critical to maintaining smooth gameplay.
High latencies can lead to frustrating lags and negatively impact the gaming experience.
Server Architecture
Understanding server models, such as peer-to-peer and client-server architectures, is essential in deciding how players connect and interact with each other and the game environment.
Bandwidth Optimization
Multiplayer games constantly exchange data between players and servers.
Efficiently managing and optimizing bandwidth usage is crucial to ensure a responsive and stable gaming experience.
Network Security
Implementing robust security measures is vital to protect the integrity of the game, prevent cheating, and safeguard players’ personal information.


Network Libraries and Middleware
Developers often utilize networking libraries and middleware that provide pre-built solutions for multiplayer functionality, saving time and effort in implementing complex networking features.

Structure of an IPv4 Address
An IPv4 address consists of a 32-bit binary number, represented in decimal format as four groups of digits separated by periods (dots).
Each group is called an octet, and it can hold values from 0 to 255.


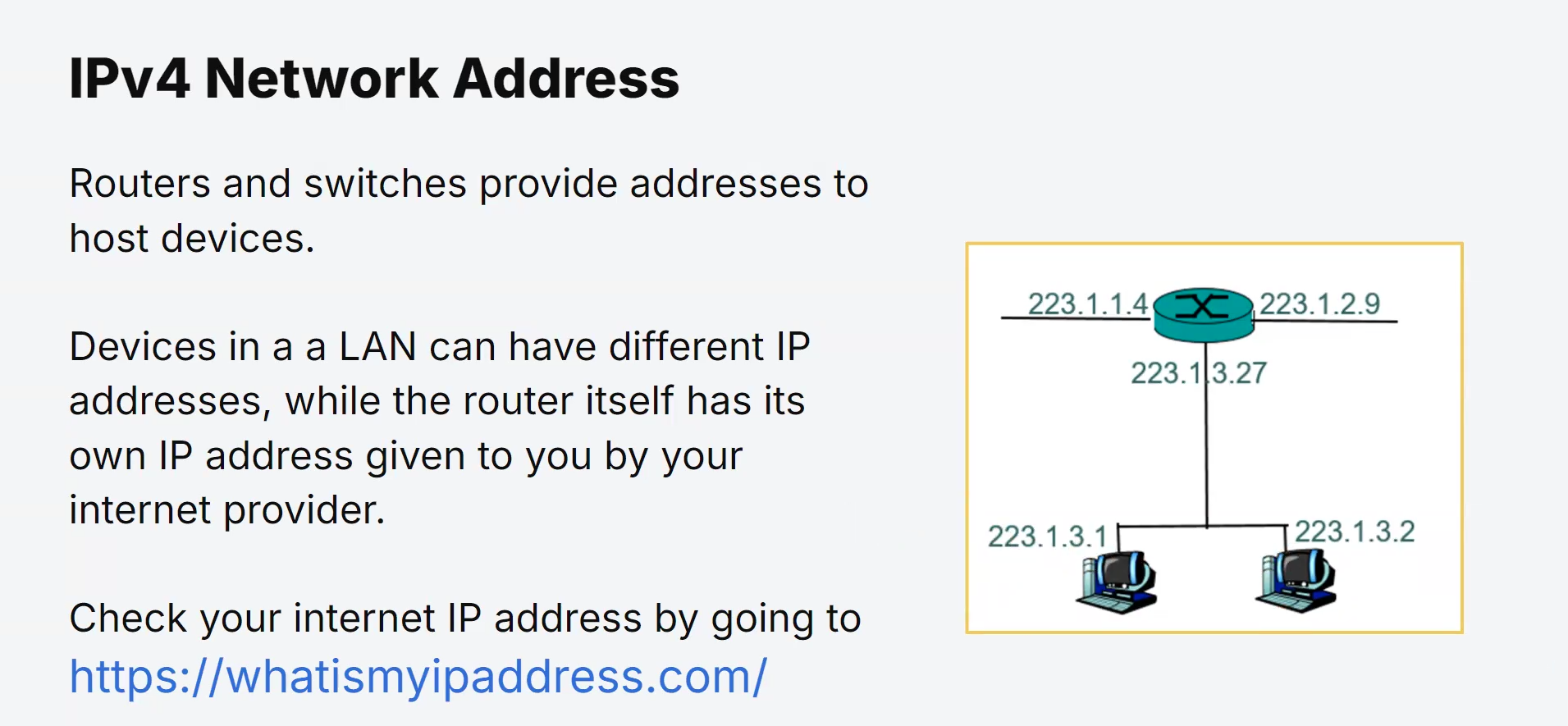

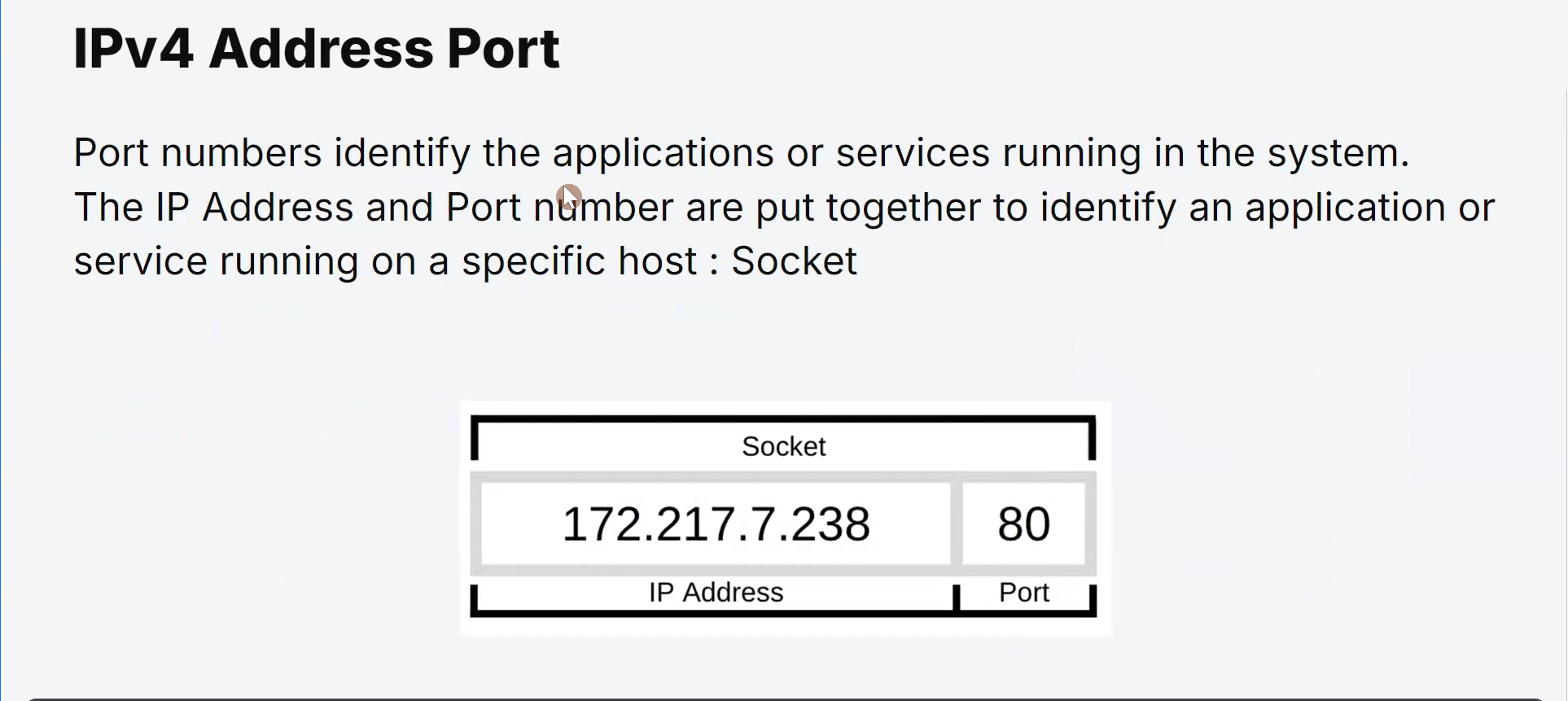
Primary purpose:
Host Identification:
Each device, such as a computer, smartphone, router, or printer, connected to a network requires a unique IPv4 address.
This address serves as an identifier for the device, allowing data packets to be sent to and received from the correct destination.
Routing Data:
When data is transmitted over a network, it is broken down into packets. These packets contain the source and destination IPv4 addresses.
Routers use this information to forward packets through various network segments until they reach their intended destination.
Routing
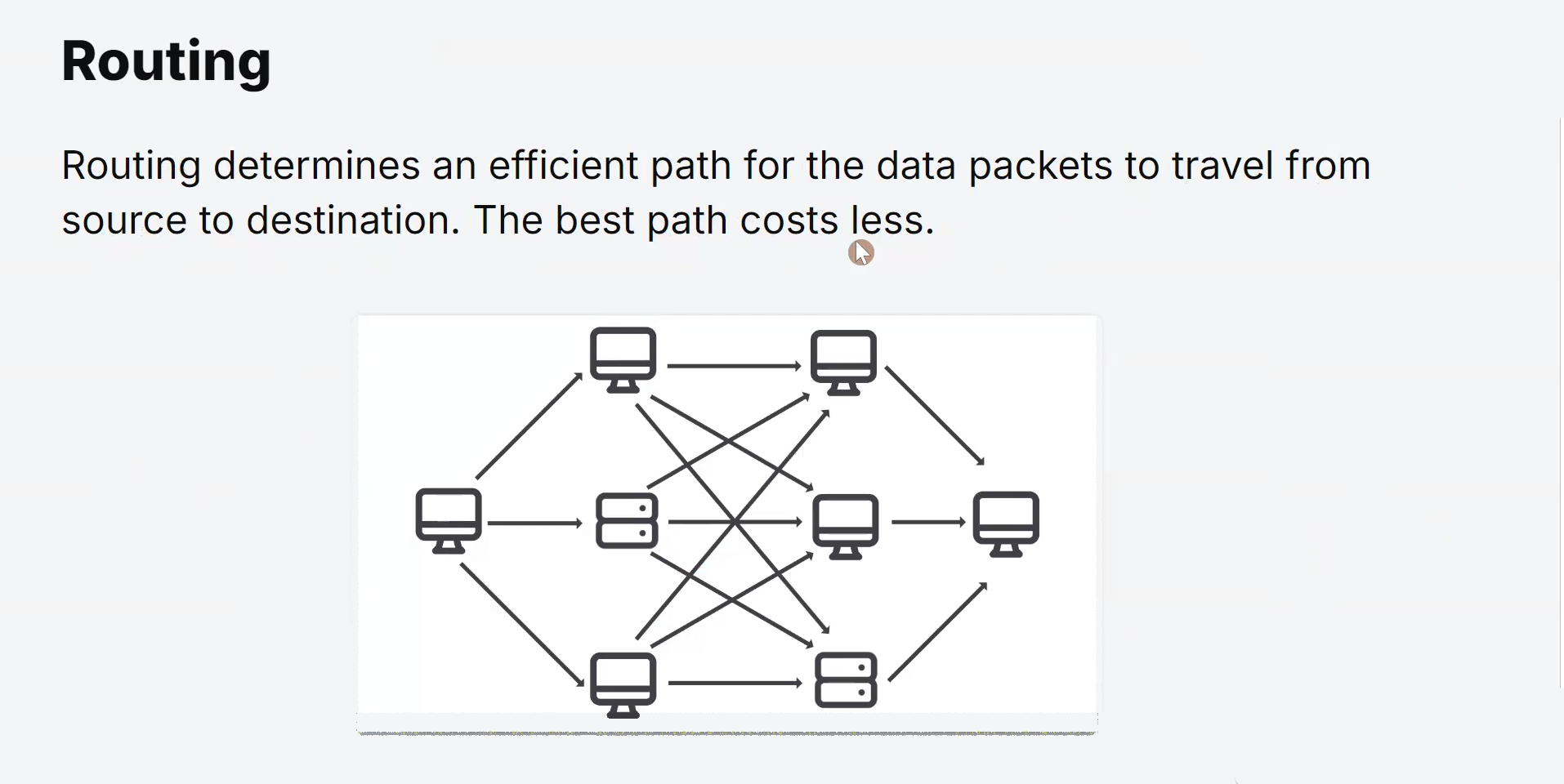
Routing is a critical process that determines how data packets are forwarded from a source device to a destination device across an interconnected network.
When data is transmitted from one device to another, it is broken down into smaller units called data packets.
These packets travel through various network devices, such as routers, switches, and gateways, based on routing decisions to reach their intended destination.
Routing relies on network protocols and algorithms to efficiently direct data packets along the optimal path to their destination.
Routers play a significant role in this process as they examine the destination IP address of each packet and make decisions on where to send it next.
They maintain routing tables that contain information about the network’s topology, allowing them to determine the best path for forwarding data.

Types of Routing
Static Routing:
In static routing, network administrators manually configure the routing tables on routers.
This approach is suitable for small, stable networks with predictable traffic patterns.
Dynamic Routing:
Dynamic routing protocols enable routers to exchange information with neighboring routers, allowing them to adapt and update their routing tables automatically.
This flexibility is ideal for larger networks with dynamic changes in network topology.
Default Routing:
Default routes are used when a router cannot find an explicit route for a packet.
They act as a “last resort” and direct packets to a predefined gateway or next hop.
Transport Protocols
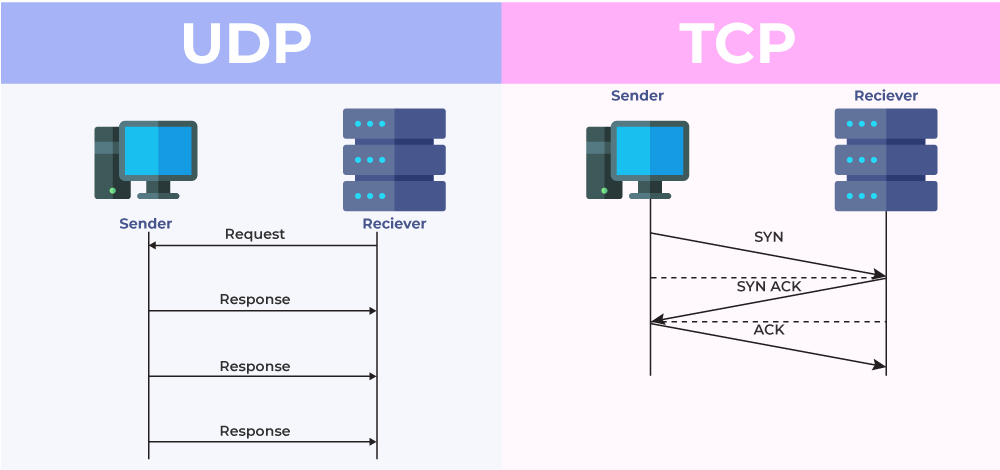
Transport protocols manage the delivery of data packets between source and destination devices.
Two primary transport protocols used in computer networks are:
Transmission Control Protocol (TCP):
TCP is a connection-oriented protocol that ensures reliable and ordered data delivery.
It establishes a virtual connection between the sender and receiver before data transmission, and acknowledgments are used to confirm successful packet delivery.
If a packet is lost, TCP will request retransmission to maintain data integrity.
The three-way handshake is necessary because both parties need to synchronize their segment sequence numbers used during their transmission.
第一次握手是传输SYN(Synchronize Sequence Number).
第二次握手是传输SYN + Acknowledgement(ACK).
第三次是ACK.
User Datagram Protocol (UDP):
UDP is a connectionless protocol that offers minimal overhead, making it suitable for real-time applications like video streaming and online gaming.
Unlike TCP, UDP does not guarantee reliable data delivery or maintain the order of packets.
However, its lower latency makes it ideal for time-sensitive applications.


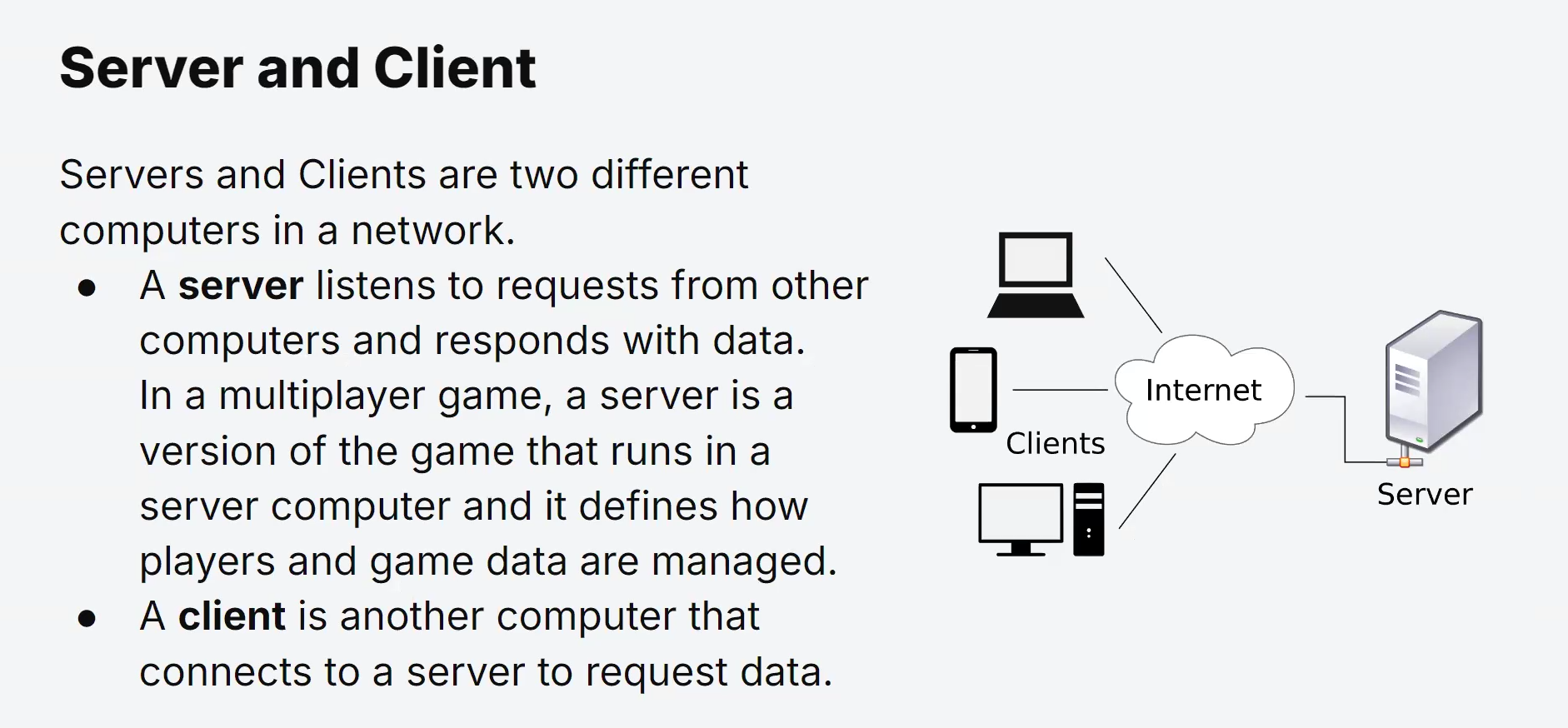
Client-Server Architecture
Client-server architecture is a widely used model in computer networking, where devices are categorized into two main roles: clients and servers.
In this model, clients request services or resources from servers, and servers provide these services in response to client requests.
This architecture allows for scalable and efficient communication between devices over a network.
Clients
Clients are the end-user devices, such as computers, smartphones, or gaming consoles, that interact with the application or service.
They initiate requests for data or actions, and upon receiving the responses from servers, they display the results to users.
Clients are responsible for providing the user interface and handling user inputs.
Servers
Servers are powerful computers or devices with high processing capabilities and ample storage.
They are responsible for hosting applications, services, or resources that clients access.
Servers process client requests, perform computations, store data, and send the results back to the clients.
Client-Server Architecture in Multiplayer Games
In the context of multiplayer games, the client-server architecture is crucial for enabling real-time interactions between players.
Here’s how it works:
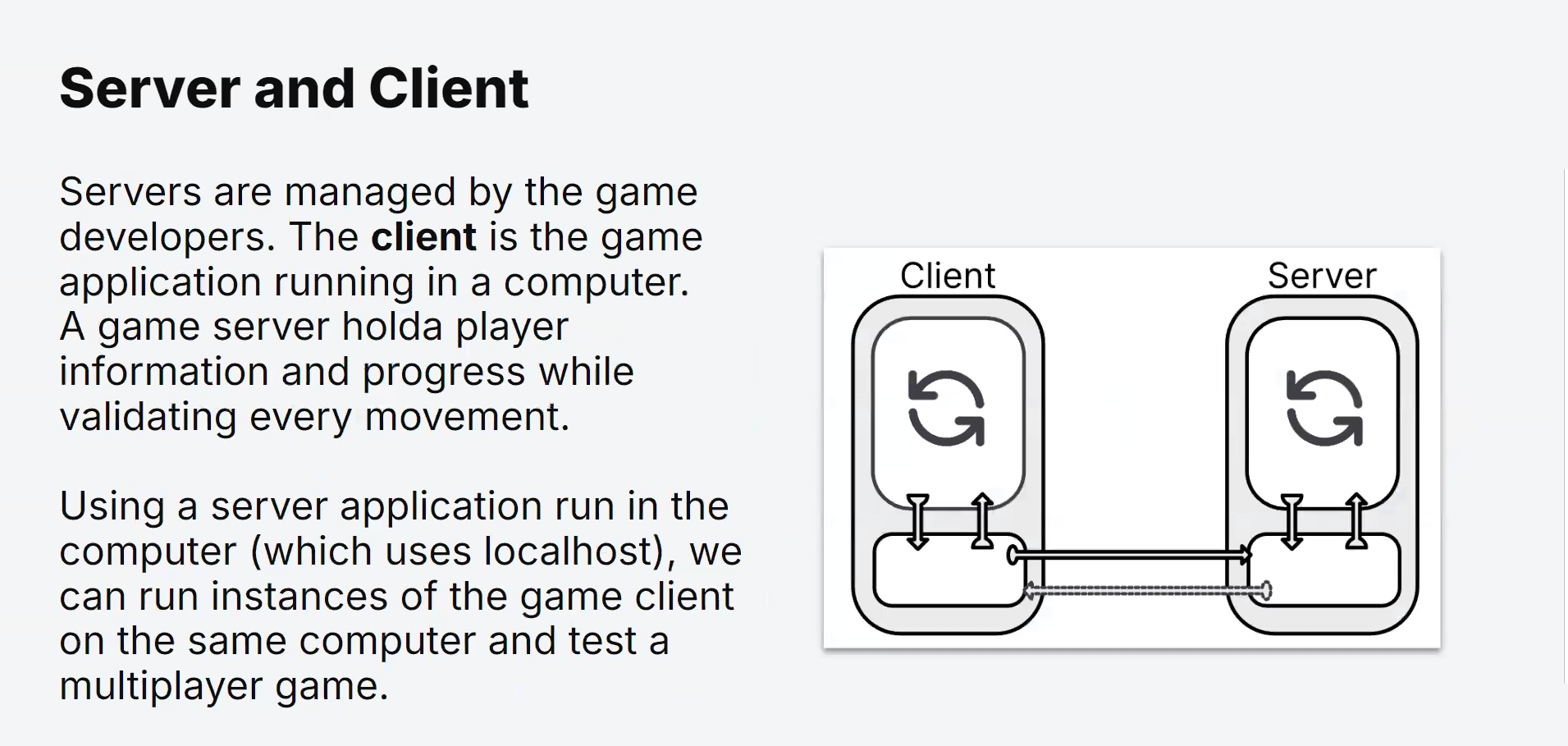
Game Servers:
In multiplayer games, dedicated game servers act as the authoritative source of game state.
These servers manage the game environment, including player positions, actions, and interactions with the game world.
Each player’s client communicates with the game server to exchange information about the game, including their actions and the actions of other players.
Client Roles:
Players’ devices (clients) connect to the game server over the network.
Each client renders the game locally on the player’s screen, handling graphics, user inputs, and local game logic.
However, critical game decisions and state information are maintained on the game server to prevent cheating and ensure consistency among all players.
Player Interactions:
When a player performs an action in the game, such as moving, shooting, or picking up an item, the client sends a request to the game server.
The server processes the action, validates it for fairness, and updates the game state accordingly.
Real-Time Updates:
The game server continuously sends updates to all connected clients, providing real-time information about the game world.
These updates include the positions and actions of other players, ensuring that every player experiences the same game environment.

Latency and Lag:
Reducing latency (the delay between sending a request and receiving a response) is crucial in multiplayer games to provide a smooth and immersive experience.
Game developers and network engineers employ various techniques to minimize lag and optimize the responsiveness of the game.
The client-server architecture offers seamless real-time interactions among players, allowing them to compete, collaborate, and immerse themselves in a shared gaming experience. This model ensures that the game environment remains fair, secure, and consistent across all players, contributing to the success and enjoyment of the multiplayer gaming experience.
Client-Server Interaction:
In an RPC setup, one device acts as the client, initiating the procedure call, while the other device functions as the server, executing the procedure requested by the client.
Marshalling and Unmarshalling:
Before transmitting the RPC request, the client’s parameters and function call are converted into a format suitable for network transmission (marshalling).
The server receives the request and converts the data back to its original format (unmarshalling) to execute the function.

Remote Procedure Execution:
The server processes the procedure call and executes the requested function using its local resources.
The results (if any) are then sent back to the client through the network.
Here’s how RPC is used in multiplayer games:
Player Actions and Synchronization:
When a player performs an action, such as shooting or moving, the client sends an RPC request to the game server, notifying it of the action taken.
Game State Updates:
The server processes these RPC requests and updates the game state accordingly.
For example, if a player moves to a new location, the server updates the player’s position in the game world.
Broadcasting Events:
RPC allows the server to broadcast important events, such as player deaths, to all connected clients.
This ensures that all players are aware of critical changes in the game environment.
Authority and Anti-Cheating Measures:
RPC helps enforce authority in multiplayer games by allowing the server to validate and execute crucial game logic.
This prevents clients from manipulating data and cheating in the game.
Minimizing Bandwidth Usage:
RPCs can be designed to send only relevant data to clients, reducing the amount of information transmitted over the network.
This optimization is essential for maintaining smooth gameplay and reducing lag.
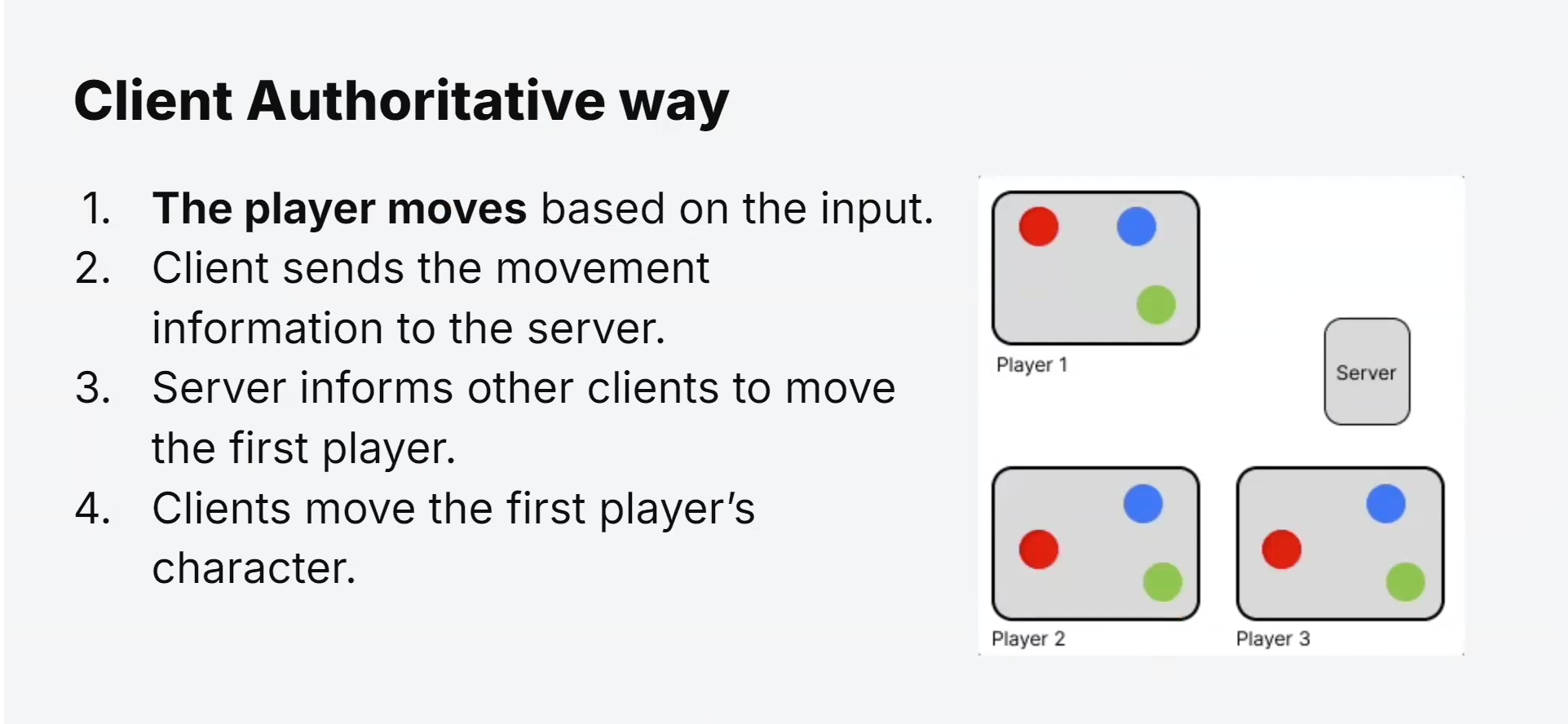
Decentralized Game Logic:
In this model, clients maintain their version of the game state and continuously send their actions to the game server.
The server receives these actions but does not actively validate or enforce them immediately.
Local Responsiveness:
Client Authoritative games offer low latency and immediate feedback to players, as the game logic is executed locally on each client.
Players experience minimal input delay and a smooth, responsive gaming experience.
Risk of Cheating:
Since clients have some authority over game logic and actions, there is a higher risk of cheating and exploiting the game.
Malicious players can manipulate their client-side data or create hacks to gain an unfair advantage.
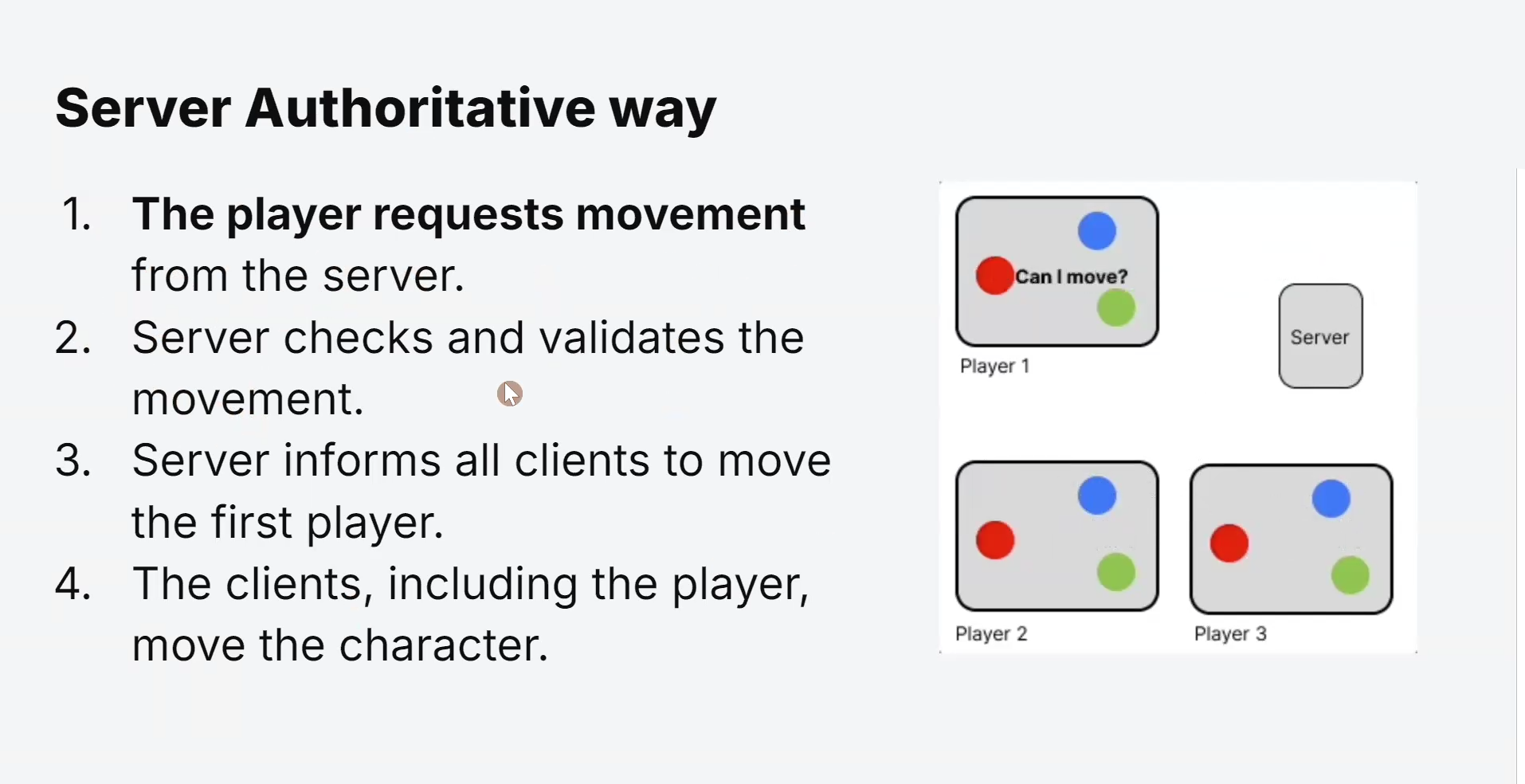
Centralized Game Logic:
In this model, the game server maintains the authoritative game state, and clients send their actions to the server for validation and execution.
Prevents Cheating:
Server Authoritative games offer better security against cheating since the server actively validates and enforces all actions.
Players cannot manipulate game logic on their clients to gain unfair advantages.
Increased Latency:
As all actions must be validated by the server, Server Authoritative games might introduce higher latency, especially if players are geographically far from the game server.
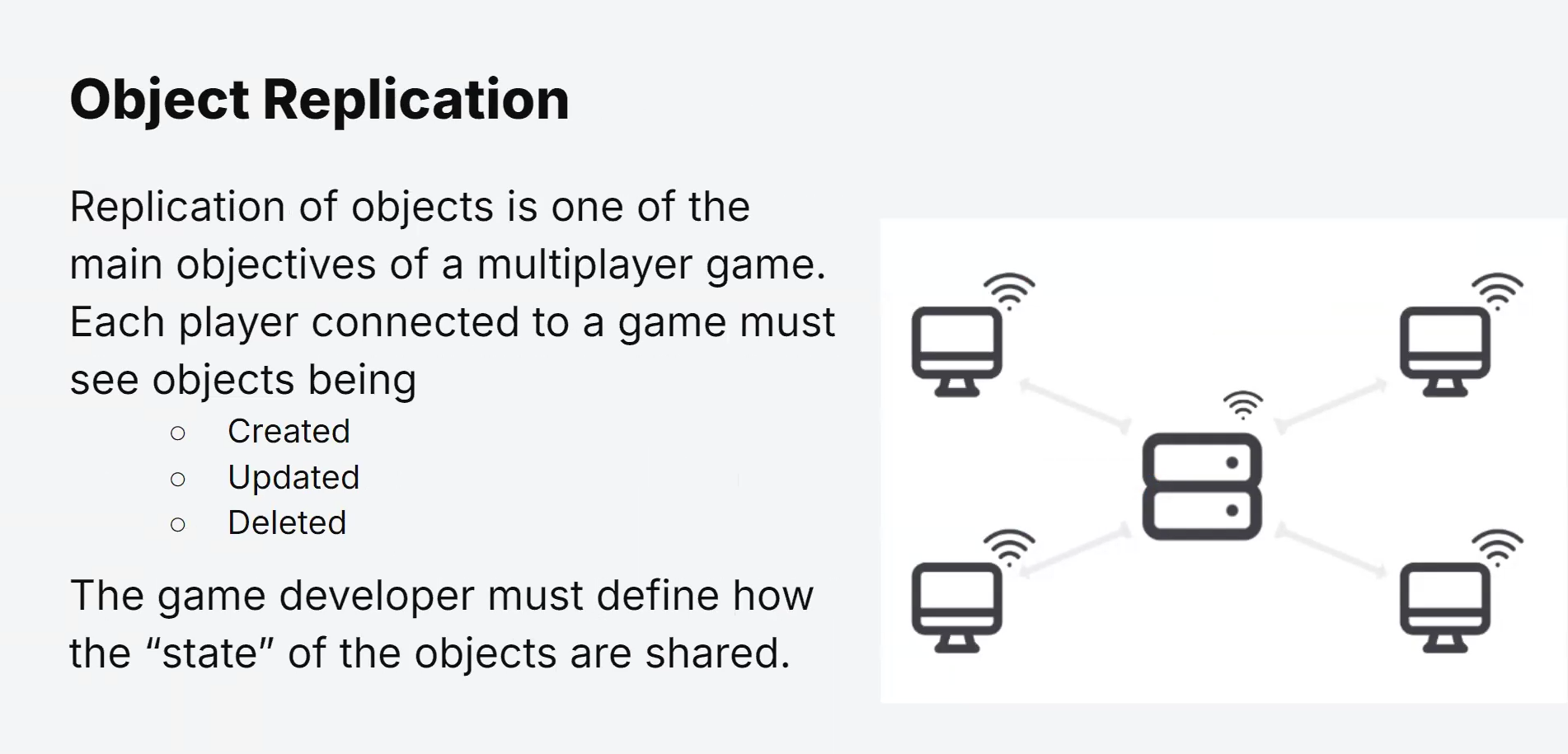

Data Packets
Data packets are the basic units of information sent across a network.
When data is transmitted over a network, it is divided into smaller, manageable pieces called data packets.
Each packet contains a header and payload.
The header includes crucial information, such as the source and destination IP addresses, packet sequence number, and other control data.
The payload contains the actual data being transmitted.


REST API
REST (Representational State Transfer) APIs are a set of conventions and guidelines that facilitate the communication and interaction between different software systems over the internet.
RESTful APIs use standard HTTP methods to perform various operations on resources, allowing clients to access and manipulate data on a server in a structured and organized manner.
API Methods
API methods define the types of actions that can be performed on resources using the RESTful API.
The four primary HTTP methods used in RESTful APIs are:
GET:
The GET method is used to retrieve data from the server.
It requests information about a resource and does not modify or alter it.
POST:
The POST method is used to create new resources on the server.
It submits data to the server to be processed and stored.
PUT:
The PUT method is used to update existing resources on the server.
It replaces the current state of a resource with the new data provided in the request.
DELETE:
The DELETE method is used to remove a resource from the server.
It instructs the server to delete the specified resource.
Terminology
Request:
A request is an HTTP message sent by the client to the server, containing information about the desired operation and any necessary data.
Response:
A response is an HTTP message sent by the server to the client in reply to a request.
It contains the requested data or the status of the requested operation.
Request or Response Headers:
Headers are additional information sent along with the request or response.
They include metadata about the data being transmitted, authentication credentials, content types, etc.
Request Body:
The request body is the data sent with a POST or PUT request.
It contains the payload or content that needs to be processed by the server.
Form-data:
Form-data is a way to send data in key-value pairs, usually associated with HTML forms.
It is commonly used in POST requests to submit form data.
Raw Data (JSON, XML, Text, etc.):
In addition to form-data, REST APIs can accept data in various formats like JSON, XML, and plain text.
JSON (JavaScript Object Notation) and XML (eXtensible Markup Language) are widely used for exchanging structured data.
Response Codes:
Response codes, also known as HTTP status codes, indicate the result of a request.
Common response codes include:
200 OK: Request was successful.
201 Created: Resource was successfully created.
204 No Content: Request was successful, but there is no data to return.
400 Bad Request: The server cannot understand the request.
401 Unauthorized: Authentication failed or user lacks permission.
404 Not Found: The requested resource could not be found.
500 Internal Server Error: An error occurred on the server-side.
Data Structure
一些过去的回忆.就只贴点图了.
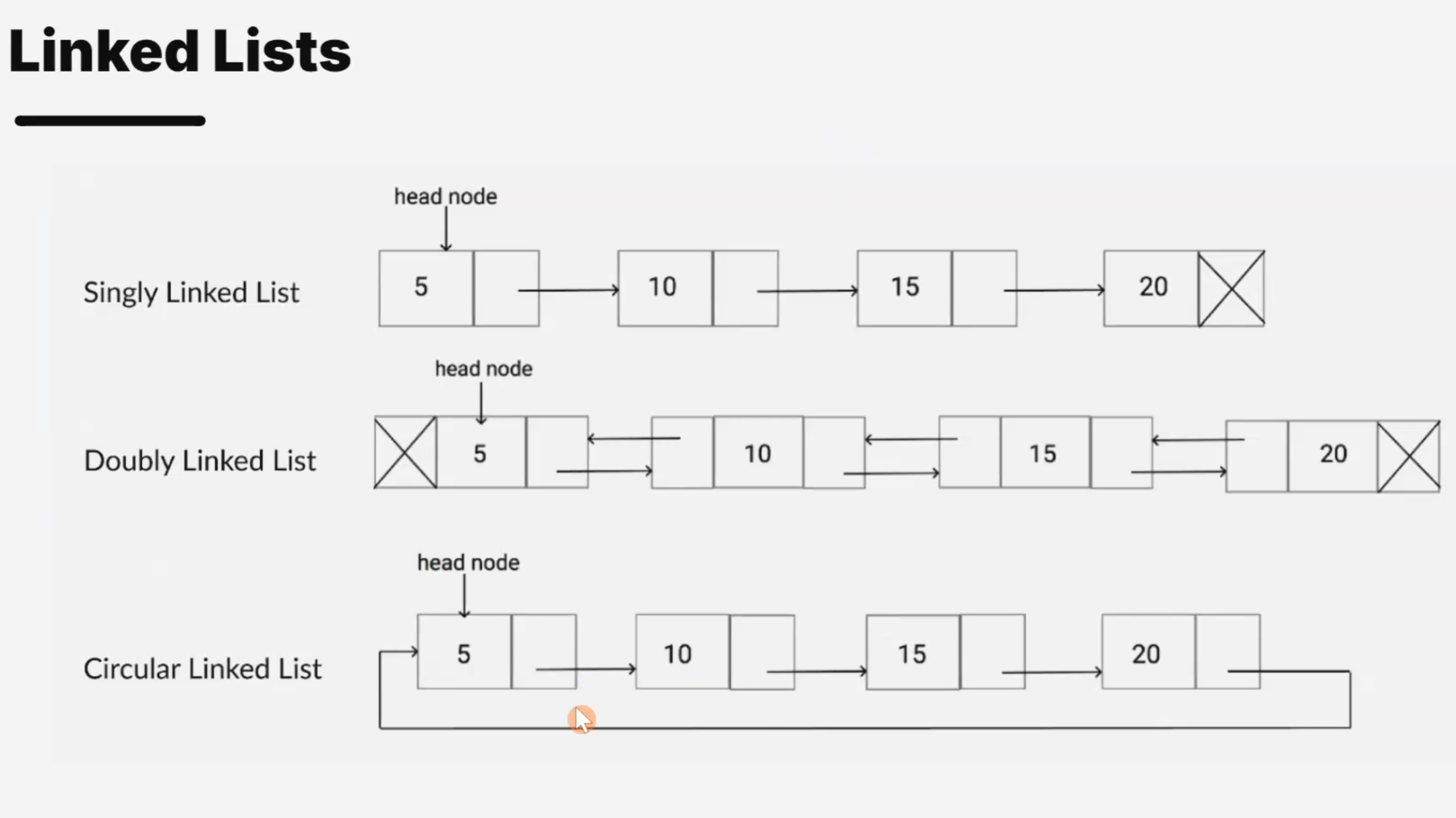
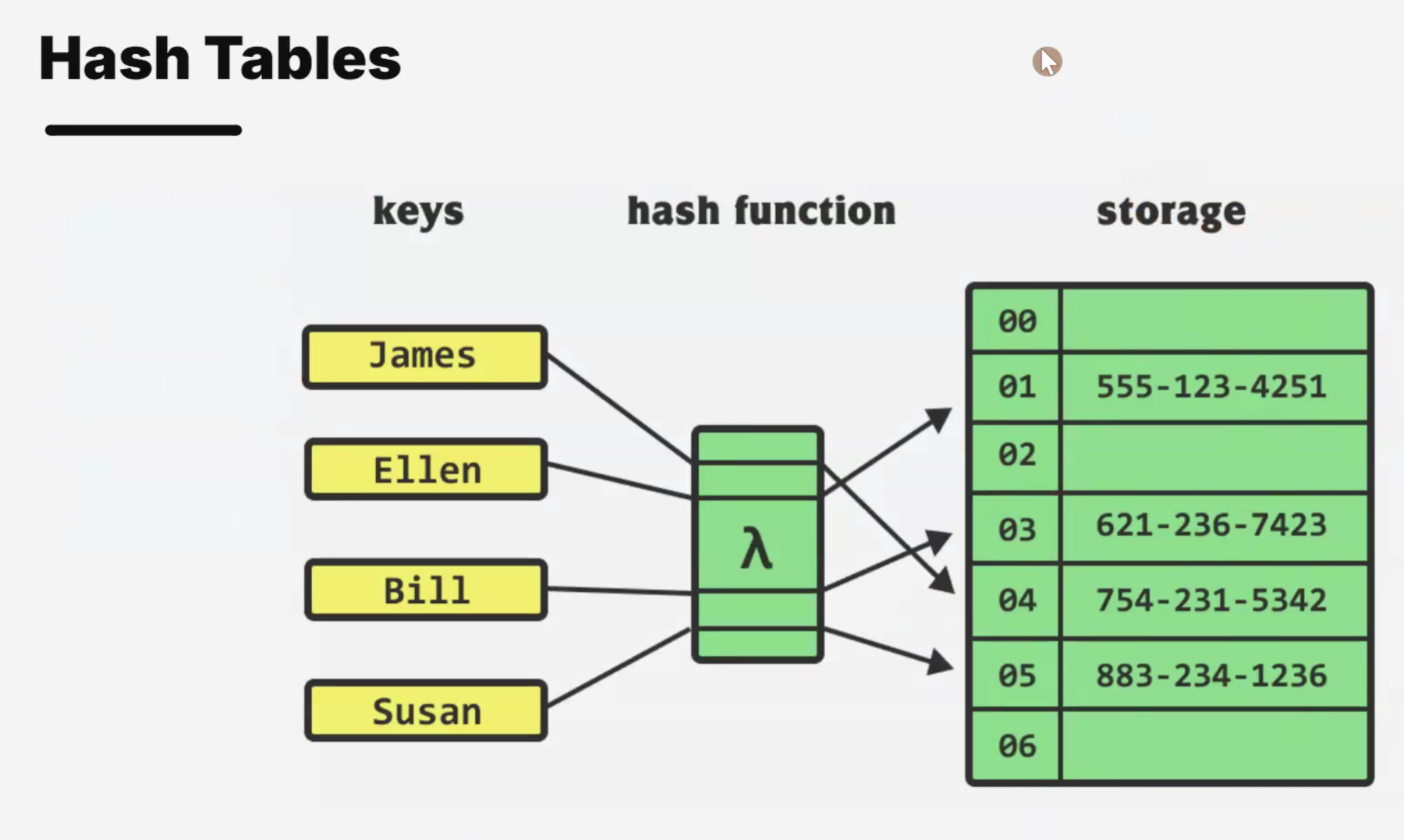
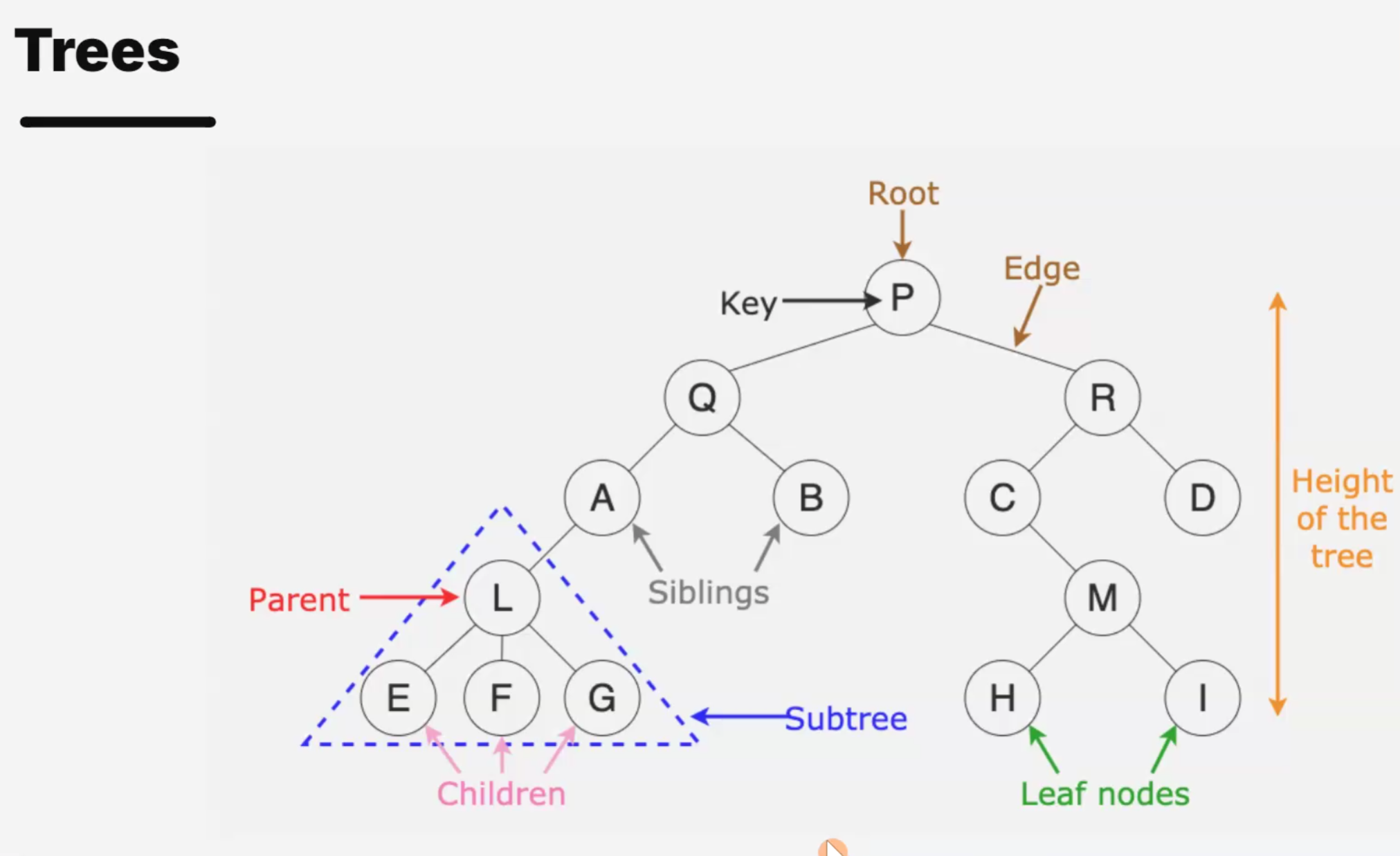

Recursive factorial function.
1 | int Factorial(int n) |
One of the most common algorithms used for finding the shortest path in graphs is Dijkstra’s algorithm.
Here’s a simplified explanation of how it works:
Start by assigning a tentative distance value to every vertex in the graph.
Set the distance of the source vertex to 0 and all other vertices to infinity.
Mark the source vertex as the current vertex.
For the current vertex, consider all of its unvisited neighbors and calculate their tentative distances by summing the distance of the current vertex and the weight of the edge between them.
If the calculated tentative distance of a neighbor is less than its current assigned distance, update the neighbor’s distance value.
Once all the neighbors of the current vertex have been considered, mark the current vertex as visited and select the unvisited vertex with the smallest tentative distance as the next current vertex.
Repeat steps 3-5 until the destination vertex is marked as visited or there are no more unvisited vertices.
The shortest path can then be reconstructed by backtracking from the destination vertex to the source vertex using the recorded distances and visited vertices.
Dijkstra’s algorithm guarantees that the shortest path is found, given that the graph doesn’t contain negative weight cycles.
It explores vertices in a greedy manner, always selecting the vertex with the smallest tentative distance as the next current vertex.
Quick Sort implementation in C#.
1 | // Function to perform Quick Sort |
What is the difference between a layer and a tag?
Layers are used to isolate things in the engine. Tags are used to label or categorize things.
- Visualization and Comparison of Sorting Algorithms
- Big O Cheat Sheet – Time Complexity Chart
- Native memory
- Install Netcode for GameObjects
- Converting IP addresses into Binary
- NetworkBehaviour spawning and despawning
- NetworkObject
- NetworkManager
- Photon
- Postman
- Weather API
Sketchpad
Windows -> package manager -> download packages的时候.
如果使用git from URL会默认到最新版本,比search更新一些.
